金属は結晶構造を有しており、金属材料のミクロな変形挙動を理解するためには結晶について学んでおく必要がある。
この記事では、一般の結晶に関する用語や結晶の分類方法について紹介する。
結晶とは
物質を構成する原子が、あるパターンをもって規則正しく配列しているような固体を結晶(crystal)と呼ぶ。
結晶を構成するもっとも基本的な構造を単位格子または単位胞という。
単位格子がどのような配置を取るかは、物質によって異なる。例えば、常温の純鉄(Fe)は体心立方格子が三次元的に配列した構造をとる(下図)。
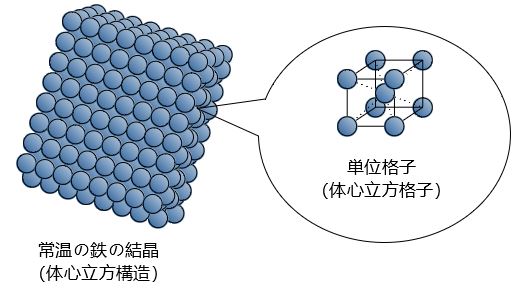
単位格子を前後上下左右に繰り返し並べていくと結晶をつくることができる。
すなわち、単位格子の分だけ原子を平行移動させたとしても、移動する前と後の結晶では見分けがつかない。
この性質を並進対称性といい、結晶を単位格子と並進対称性によって定義することもできる。
単位格子は平行六面体となる。
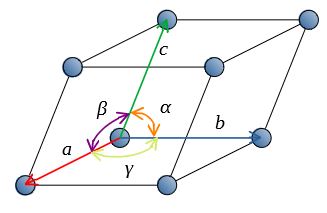
この平行六面体を特徴付ける、3つの軸の長さ\((a,b,c)\)および角\((\alpha,\beta,\gamma)\)を格子定数という。
格子定数の間の関係から、単位格子のもつ対称性によって次に述べるような結晶系に分類することができる。
結晶系とブラベー格子
単位格子の中に原子1個だけ含むものを、単純格子と呼ぶ。
単純な単位格子のみが持つ対称性によると、7種類の結晶系に分類することができる。
また、単純格子に加えて格子の中心あるいは面の中心にも原子を配置した構造を考えると、並進対称性を考慮して14種類に分類することができる。これをブラベー格子(Bravais Lattice)と呼ぶ。
結晶系とブラベー格子の一覧を以下にまとめる。
| 結晶系 | 格子定数 | ブラベー格子 (左から 単純(P)/底心(C)/体心(I)/面心(F) 格子) |
| 三斜晶系 (a) triclinic |
\(a\ne b\ne c \\ \alpha\ne\beta\ne\gamma\) |  |
| 単斜晶系 (m) monoclinic |
\(a\ne b\ne c \\ \alpha=\beta=90^{\circ},\gamma\ne90^{\circ}\) | 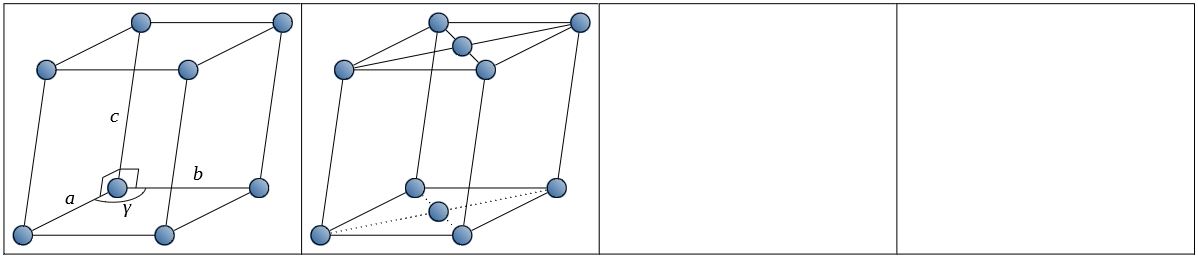 |
| 直方晶系 (o) (斜方晶系) orthorhombic |
\(a\ne b\ne c \\ \alpha=\beta=\gamma=90^{\circ}\) | 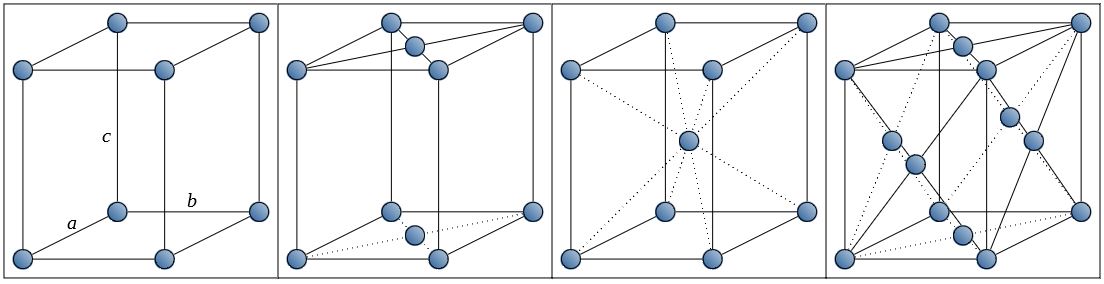 |
| 六方晶系 (h) hexagonal |
\(a= b\ne c \\ \alpha=\beta=90^{\circ},\gamma=120^{\circ}\) |  |
| 三方晶系 (h) (菱面体晶系) rhombohedral |
\(a= b= c \\ \alpha=\beta=\gamma \ne90^{\circ}\) |
 |
| 正方晶系 (t) tetragonal |
\(a= b\ne c \\ \alpha=\beta=\gamma =90^{\circ}\) |
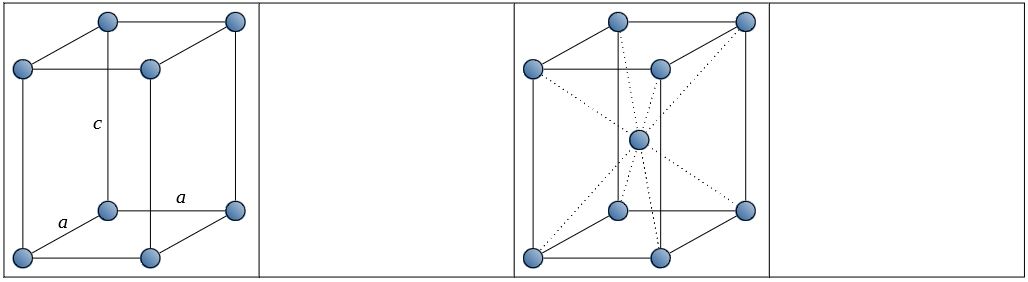 |
| 立方晶系 (c) cubic |
\(a= b= c \\ \alpha=\beta=\gamma =90^{\circ}\) |
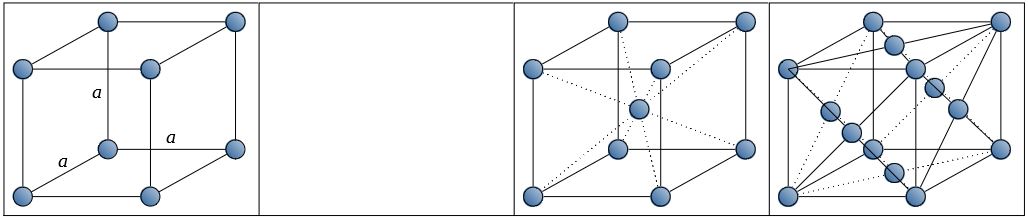 |
下の結晶系ほど対称性が高い。
ピアソン記号
上の表において、かっこ内の英字はピアソン記号と呼ばれる結晶構造の表記法を示している。
| 記号 | 結晶系 | 記号 | 格子系 |
| a | 三斜晶 | P | 単純格子 |
| m | 単斜晶 | C | 底心格子 |
| o | 直方晶 | I | 体心格子 |
| h | 六方晶、三方晶 | F | 面心格子 |
| t | 正方晶 | ||
| c | 立方晶 |
ピアソン記号を用いると、例えば単純正方格子は「tP」、面心立方格子は「cF」のように表される。
面心正方格子が含まれない理由
図を描いてみると理解しやすい。
面心正方格子を二つ並べる。
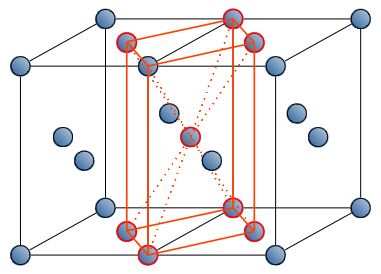
すると、真ん中に格子定数が\(a/\sqrt{2}\)の体心正方格子が現れる。
体心正方格子の方がより基本的な構造であり、並進対称性を考慮すると面心正方格子はブラベー格子には含まれない。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]




