前回の記事では結晶の基本構造について学んだ。
[mathjax] 金属は結晶構造を有しており、金属材料のミクロな変形挙動を理解するためには結晶について学んでおく必要がある。 この記事では、一般の結晶に関する用語や結晶の分類方法について紹介する。 結晶とは 物質を構成する[…]
金属材料の変形を結晶の観点から理解するために、もうひとつ準備をしておきたい。
それは、結晶中の面や方向を表記する方法である。
結晶は同じ構造が無数に並んでいるため、通常の固定座標を適用するのは不便である。そこで用いられるのが、ミラー指数と呼ばれる表記法である。
この記事では、ミラー指数を用いて面や方向をどのように表すかを学ぶ。
なお、ほとんどの金属は面心立方構造・体心立構造・六方最密充填構造のいずれかの構造を取るため、以下では立方晶および六方晶について考えることにする。
立方晶のミラー指数
結晶格子中の面や方向を、次のように表す。
なおミラー指数では括弧の種類が意味を持つため、区別して理解すること。
格子定数を\(a\)とし、単位格子の3つの結晶軸を座標軸にとる。
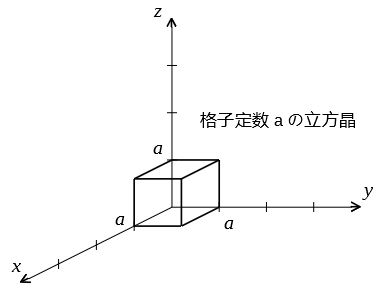
方向の表し方
原点から点\((H,K,L)\)へ向かう方向は
\(H:K:L\)の最小の整数比\(h:k:l\)を用いて\([hkl]\)と表す。
ただし、負の数の場合は数字の上にバーを付けて\([\bar{h}kl]\)のように書き、「\(バーhkl方向\)」のように読む。
原点から点\((4,0,-2)\)に向かう方向は、\([20\bar{1}]\)とかく。
代表的な方向の例を図示する。
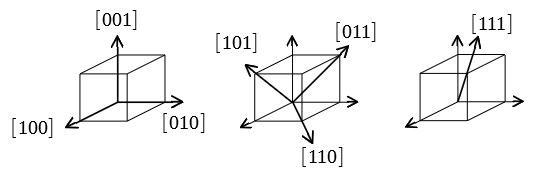
面の表し方
表したい面と、各座標軸の交点\((H,K,L)\)を求める。それぞれを格子定数で割り、その逆数
$$\frac{a}{H}:\frac{a}{K}:\frac{a}{L}$$
の最小の整数比\(h:k:l\)を用いて\((hkl)\)と表す。
負の数については方向の時と同じくバーを付けて\((\bar{h}kl)\)のように書き、「\(バーhkl面\)」という。
例:\(x軸とa,y軸とa,z軸と2a\)で交点を持つ面は
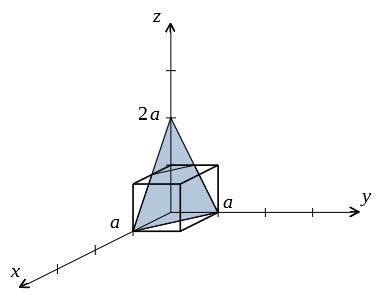
格子定数で割って、その逆数の整数比を求める。
$$\frac{a}{a}:\frac{a}{a}:\frac{a}{2a}=1:1:\frac{1}{2}=2:2:1$$
よってこの面のミラー指数は\((221)\)である。図示すると下図の青ハッチング部となる。
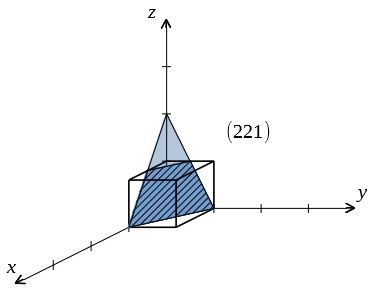
面がある軸と交わらないとき、その軸の指数はゼロとする。これは無限遠で交わると考えて、その逆数\(\frac{1}{\infty}=0\)をとったとみなす。
例えば、\(x軸とa,y軸とa\)で交点を持ち、z軸と平行な面は
$$\frac{1}{1}:\frac{1}{1}:\frac{1}{\infty}=1:1:0$$
から\((110)\)面となる。
代表的な面の例を図示する。
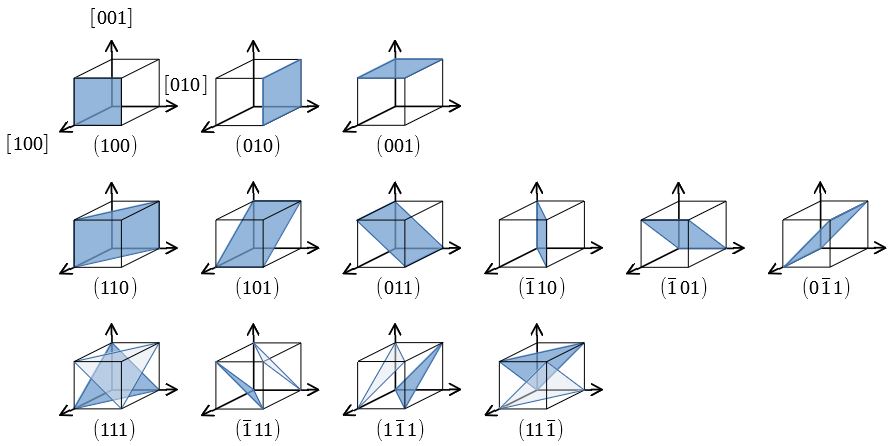
等価な面・方向の表し方
結晶格子の対称性から、等価な面や方向が複数存在する場合がある。
これらをまとめて表記したいときは、以下のように記述する。
$$\{100\}=(100),(010),(001),(\bar{1}00),(0\bar{1}0),(00\bar{1})$$
$$<\!\!100\!\!>=[100],[010],[001],[\bar{1}00],[0\bar{1}0],[00\bar{1}]$$
面のなす角・面間隔の公式
ミラー指数を用いると、面や方向に関する計算を容易に行うことができる。
立方晶では、\([hkl]\)方向は\((hkl)\)面の法線方向になる。
\((h_1k_1l_1)\)面と\((h_2k_2l_2)\)面のなす角\(\theta\)は、\([h_1k_1l_1]\)方向と\([h_2k_2l_2]\)方向のなす角に等しく
$$\cos\theta=\frac{h_1h_2+k_1k_2+l_1l_2}{\sqrt{h_1^2+k_1^2+l_1^2}\sqrt{h_2^2+k_2^2+l_2^2}}$$
で与えられる。
\((hkl)\)面の方程式は\(hx+ky+lz-a=0\)である。
この面と原点の距離が\((hkl)\)面の面間隔\(d_{hkl}\)に等しく
$$d_{hkl}=\frac{a}{\sqrt{h^2+k^2+l^2}}$$
で与えられる。
\((hkl)\)面の面間隔\(d_{hkl}\)と、ミラー指数を\(n\)倍した\((nh~nk~nl)\)面の面間隔\(d_{nhkl}\)には次の関係が成り立つ。
\begin{align*}
d_{nhkl}&=\frac{a}{\sqrt{(nh)^2+(nk)^2+(nl)^2}} \\
&=\frac{a}{n\sqrt{h^2+k^2+l^2}} \\
&=\frac{d_{hkl}}{n}
\end{align*}
\(\{200\}\)面の間隔は\(\{100\}\)面の間隔の半分である。
ミラー指数が\(n\)倍になると、面間隔は\(n\)分の1になる。
六方晶のミラー指数
軸が4本\((a_1,a_2,a_3,c)\)ある点で立方晶と異なるが、基本的なルールは同様である。
\((a_1,a_2,a_3)\)軸が互いに\(120^{\circ}\)で交わることから、これら三方向を示す指数\(h,k,l\)には、\(h+k=-l\)の関係がある。
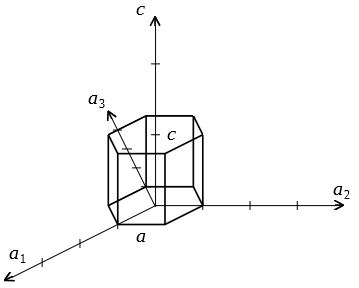
格子定数は\(a,c\)とする。
方向の表し方
\(a_1,a_2,c\)軸座標において、原点から点\((H,K,M)\)へ向かう方向は
\(H:K:L\)の最小の整数比\(h:k:m\)を求め、残りの指数は\(l=-(h+k)\)により定める。
例:\(a_1\)軸方向のミラー指数
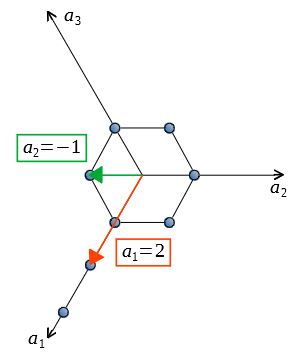
\(h:k:m=2:-1:0\)および\(l=-2+1=-1\)
よって\([2\bar{1}\bar{1}0]\)方向となる。
方向の例を図示する。
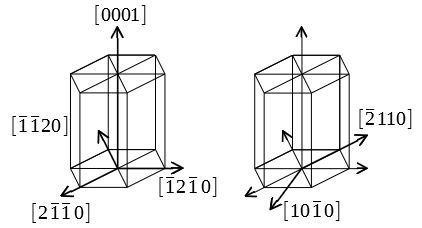
面の表し方
表したい面と、\(a_1,a_2,c\)軸の交点\((H,K,M)\)を求める。それぞれを格子定数で割り、その逆数
$$\frac{a}{H}:\frac{a}{K}:\frac{c}{M}$$
の最小の整数比\(h:k:m\)を求め、残りの指数は\(l=-(h+k)\)により定める。
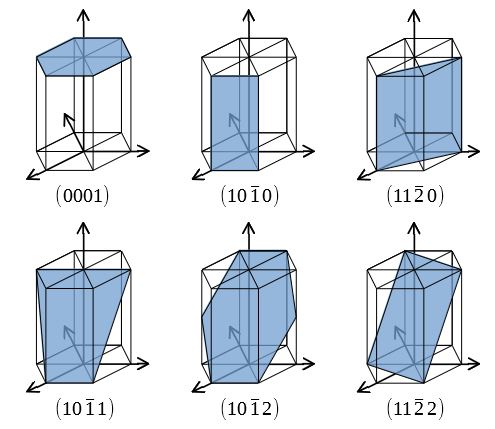
代表的な面を図示する。
面のなす角・面間隔の公式
六方晶では、\(c\)軸に平行な面以外では\([hklm]\)方向と\((hklm)\)面は直交しない。
また4つのミラー指数の内、計算で求める三番目の指数\(l\)は利用しない。
\((h_1k_1l_1m_1)\)面と\((h_2k_2l_2m_2)\)面のなす角\(\theta\)は
$$\cos\theta=\frac{h_1h_2+k_1k_2+\displaystyle\frac{1}{2}(h_1k_2+h_2k_1+)+\frac{3}{4}\left(\frac{a}{c}\right)^2m_1m_2}{\sqrt{h_1^2+k_1^2+h_1k_1+\displaystyle\frac{3}{4}\left(\frac{a}{c}\right)^2m_1^2}\sqrt{h_2^2+k_2^2+h_2k_2+\displaystyle\frac{3}{4}\left(\frac{a}{c}\right)^2m_2^2}}$$
で与えられる。
また\((hklm)\)面の面間隔\(d_{hklm}\)は
$$d_{hklm}=\frac{a}{\sqrt{\displaystyle\frac{4}{3}(h^2+hk+k^2)+\displaystyle\left(\frac{a}{c}\right)^2m^2}}$$
で与えられる。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]




