物体に働く応力は「体積変化」のみに寄与する成分と「形状変化」のみに寄与する成分にわけることができ、前者を静水圧応力、後者を偏差応力という。
塑性変形においては静水圧の影響は無視できると考えられるため、偏差応力を利用して理論が展開される。
この記事は、静水圧応力および偏差応力の定義と考え方を学び、偏差応力テンソルの不変量を導く。これは後に学ぶ降伏条件で登場する。
静水圧応力
流体中の物体は、その表面に垂直な方向に圧力を受ける。この圧力は物体の体積を変化させる役割を果たすが、形状変化には関係がない。
応力テンソルでいえば、垂直応力成分がこの働きをする。
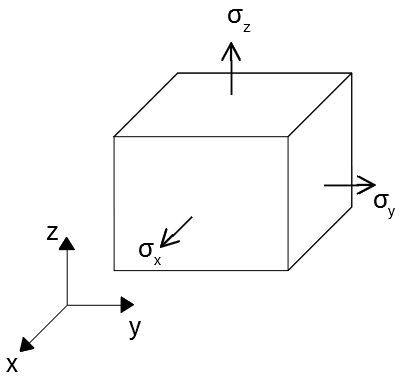
そこで、3つの垂直応力成分の平均値をとった
$$\sigma_m=\frac{1}{3}\sigma_{ii}=\frac{1}{3}(\sigma_{x}+\sigma_{y}+\sigma_{z})$$
を静水圧応力(hydrostatic stress)または平均垂直応力(mean normal stress)と呼ぶ。
体積弾性率
一様な圧力\(p\)が作用しているときの静水圧応力は
$$\sigma_m=\frac{1}{3}(-p-p-p)=-p$$
となる。
さらに、圧力\(p\)と体積ひずみ\(\varepsilon_V=\Delta V/V\)の関係は
$$p=-K\varepsilon_V$$
で定義される。この\(K\)を体積弾性率(bulk modulus)といい、次の関係式が成り立つ。
$$K=\frac{E}{3(1-2\nu)}=\frac{3\lambda+2\mu}{3}$$
ここで\(E\)はヤング率、\(\nu\)はポアソン比、\(\lambda,\mu\)はラメの定数である。
偏差応力
応力テンソルの各垂直応力成分から静水圧応力を差し引いた
$$\boldsymbol{\sigma}^{\prime}=\sigma_{ij}^{\prime}=\sigma_{ij}-\sigma_m\delta_{ij}$$
を偏差応力(deviatoric stress)テンソルと呼ぶ。ただし\(\delta_{ij}\)はクロネッカーのデルタである。
行列の形で書き下せば
\[\left(
\begin{array}{ccc}
\sigma_x-\frac{\sigma_{x}+\sigma_{y}+\sigma_{z}}{3} & \tau_{xy} & \tau_{xz} \\
\tau_{yx} & \sigma_y-\frac{\sigma_{x}+\sigma_{y}+\sigma_{z}}{3} & \tau_{yz} \\
\tau_{zx} & \tau_{zy} & \sigma_z-\frac{\sigma_{x}+\sigma_{y}+\sigma_{z}}{3}
\end{array}
\right)\]
となる。
一様な圧力の下では垂直成分はゼロになり、塑性変形はしない。一方、一軸引張では垂直成分が値を持ち、塑性変形が起こる。
不変量
の定義から、偏差応力テンソルの不変量\(J_1,J_2,J_3\)を計算してみよう。
\begin{align*}
J_1&=\mathrm{tr}(\boldsymbol{\sigma}^{\prime})=\sigma_x+\sigma_y+\sigma_z-3\sigma_m=0 \\
J_2&=-\left\{(\sigma_x-\sigma_m)(\sigma_y-\sigma_m)+(\sigma_y-\sigma_m)(\sigma_z-\sigma_m)+(\sigma_z-\sigma_m)(\sigma_x-\sigma_m)\right\}+\tau_{xy}^2+\tau_{yz}^2+\tau_{zx}^2 \\
&=-\left(\sigma_x\sigma_y+\sigma_y\sigma_z+\sigma_z\sigma_x-2\sigma_x\sigma_m-2\sigma_y\sigma_m-2\sigma_z\sigma_m+3\sigma_m^2\right)+\tau_{xy}^2+\tau_{yz}^2+\tau_{zx}^2 \\
&=\displaystyle\frac{1}{3}\left(\sigma_x^2+\sigma_y^2+\sigma_z^2-\sigma_x\sigma_y-\sigma_y\sigma_z-\sigma_z\sigma_x+3\tau_{xy}^2+3\tau_{yz}^2+3\tau_{zx}^2\right) \\
J_3&=\mathrm{det}(\boldsymbol{\sigma}^{\prime})
\end{align*}
これらの値は座標系によらず一定の値を持つ。
特に、2次の不変量\(J_2\)はミーゼスの降伏条件式にも登場する。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]




