金属材料の塑性変形は、転位の運動により原子の位置が動くために生じる。これをすべり変形という。
すべり変形に必要な応力や変形方向、メカニズムを理解するためには、結晶構造に基づいて考える必要がある。
ここでは、すべり変形の基礎を学ぶ。
すべり系
単結晶材を一軸で引張ると、ある面に沿ってある方向にすべりが発生する。
すべりが発生する面をすべり面、移動方向をすべり方向といい、ふたつの組み合わせをすべり系(slip system)と呼ぶ。
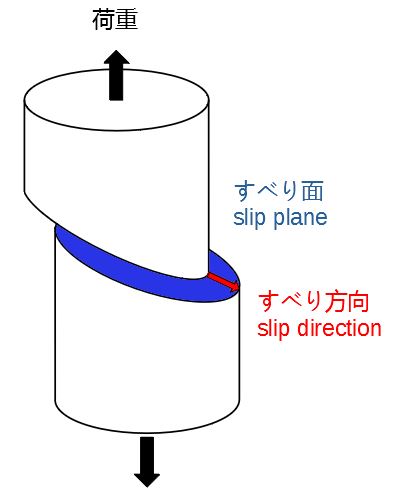
すべり面は面間隔が最大となる最密面、すべり方向は最も近い原子同士を結ぶ最密方向になる。
すなわち、すべり系は結晶学的に決定される。
金属の結晶構造と代表的なすべり系を下表にまとめる。ミラー指数については前回の記事を参照。
| 結晶構造 | 金属の例 | すべり面 | すべり方向 | すべり系の数 |
| 面心立方格子 (fcc) |
Al、Cu、Au、Agなど | \(\{111\}\) | \(<\!\!110\!\!>\) | \(4\times3=12\) |
| 体心立方格子 (bcc) |
α-Fe、W、Mo、Crなど | \(\{110\}\) \(\{112\}\) \(\{123\}\) |
\(<\!\!111\!\!>\) | \(6\times2=6\) \(12\times1=12\) \(24\times1=24\) |
| 最密六方格子 (hcp) |
Mg、Ti、Znなど | \((0001)\) \(\{10\bar{1}0\}\) \(\{10\bar{1}1\}\) |
\(<\!\!11\bar{2}0\!\!>\) | \(1\times3=3\) \(3\times1=3\) \(6\times1=6\) |
各構造について詳細をみていこう。
fcc金属のすべり系
fcc金属は4つの等価な\(\{111\}\)すべり面と、ひとつの面内に3つの等価な\(<\!\!110\!\!>\)すべり方向を持つ。
例えば下図に示すように、\((111)\)面には\([\bar{1}10],[10\bar{1}],[0\bar{1}1]\)のすべり方向がある。
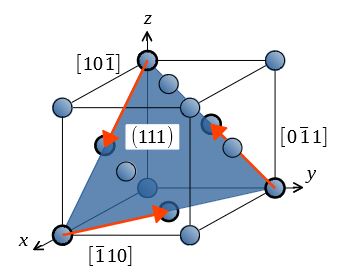
したがって、fcc金属の\(\{111\}<\!\!110\!\!>\)すべり系の数は\(4\times3=12\)個である。
bcc金属のすべり系
bcc金属のすべり系はfccに比べてやや複雑である。
bcc金属で主に働くと考えられているのは、\(\{110\},\{112\},\{123\}\)の3種類のすべり面と、格子点の原子と体心原子を結ぶ\(<\!\!111\!\!>\)方向からなるすべり系である。
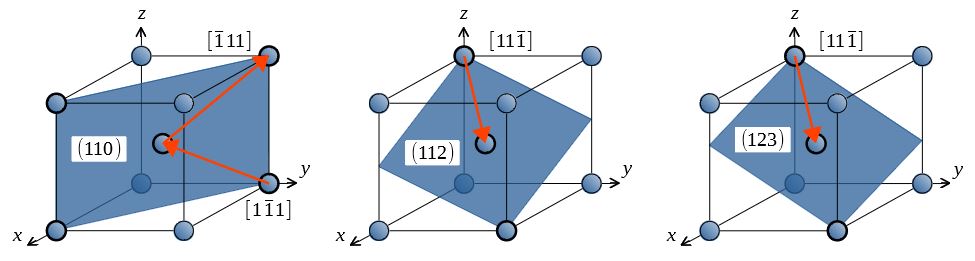
上の表に示したように、各すべり系の数は6、12、24個である。
hcp金属のすべり系
hcp金属では、底面\((0001)\)・柱面\(\{10\bar{1}0\}\)・錐面\(\{10\bar{1}1\}\)の3種類のすべり面がある。
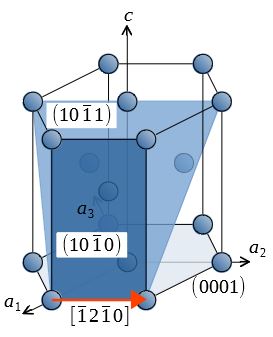
なお、hcp金属は軸比や負荷経路によって活動すべり系および双晶系が異なるので注意する。
柱面すべりおよび錐面すべりは一般に活動しにくく、底面すべりが主すべり系となる。
すなわちhcp金属では活動すべり系の数が\(1\times3=3\)個と少ないため、塑性変形しにくいという特徴がある。
これを補うために双晶変形が大きな役割を果たす場合も多い。
分解せん断応力とシュミット因子
次に、金属材料に対して外力を与えたときに「どのすべり系が活動するか」を考えよう。
すべり変形は、すべり面に沿ってせん断変位が発生することで生じるため、外力をせん断応力に分解することからはじめる。
円柱状の単結晶材の一軸引張を考える。
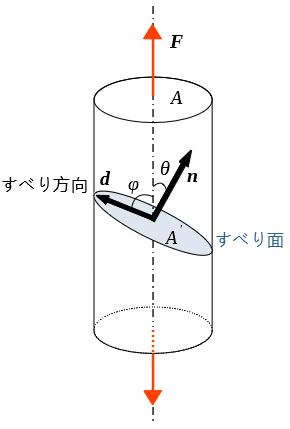
軸方向の引張り力を\(\boldsymbol{F}\)、軸に垂直な面の断面積を\(A\)、すべり面の法線を\(\boldsymbol{n}\)、すべり方向を\(\boldsymbol{d}\)とする。
\(\boldsymbol{F}\)と\(\boldsymbol{n}\)のなす角を\(\theta\)、\(\boldsymbol{F}\)と\(\boldsymbol{d}\)のなす角を\(\phi\)とする。
引張応力\(\sigma\)は、引張り力の大きさを\(F\)とすると
$$\sigma=\frac{F}{A}$$
である。また、すべり面\(A^{\prime}\)の面積は
$$A^{\prime}=\frac{A}{\cos\theta}$$
で与えられる。さらに\(\boldsymbol{F}\)のすべり方向成分は\(F\cos\phi\)であることから、このすべり系に作用する分解せん断応力\(\tau\)は
$$\tau=\frac{F\cos\phi}{A^{\prime}}=\frac{F}{A}\cos\theta\cos\phi=\sigma\cos\theta\cos\phi$$
となる。ここに登場する\(S_F=\cos\theta\cos\phi\)をシュミット因子(Schmid factor)という。
この式から、次のことがわかる。
- シュミット因子の絶対値\(|S_F|\)が大きいほど、分解せん断応力\(\tau\)も大きくなる
- すべり面と外力が平行\((\theta=90^{\circ})\)なとき、このすべり系に作用するせん断応力は生じない
- すべり方向と外力が垂直\((\phi=90^{\circ})\)なとき、このすべり系に作用するせん断応力は生じない
\(|S_F|\)が最大となるすべり系を主すべり系といい、塑性変形が開始するときまずはじめに活動する。
なお、シュミット因子は\(\theta=\phi=45^{\circ}\)のとき最大値\(0.5\)をとる。
シュミットの法則
単結晶材において、主すべり系の分解せん断応力がある一定値\(\tau_{C}\)に達したときにすべり変形が開始する。これをシュミットの法則(Schmid’s law)という。
このときのせん断応力を臨界分解せん断応力(CRSS: critical resolved shear stress)といい、降伏応力\(\sigma_Y\)との間に次の関係が成り立つ。
$$\sigma_Y=\frac{\tau_{C}}{\cos\theta\cos\phi}$$
この関係はfcc金属やhcp金属でよく成り立つことが知られている。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]





