ここでは、工学的によく用いられる応力とひずみの定義、計算方法について解説する。
応力やひずみには用途に応じて様々な種類がある。
以下では、垂直応力・ひずみとせん断応力・ひずみの定義、公称応力と真応力、真ひずみ(対数ひずみ)といった用語について理解することを目的とする。
なお、応力テンソル・ひずみテンソルについては別の記事を作成予定である。
応力・ひずみとは
まずは、応力(stress)とひずみ(strain)とは何かについて簡単に述べておく。
応力とは、「物体に外部から力を加えたときに物体の内部に発生する単位面積当たりの力」をいう。
ここで特に重要なのは、単位面積当たりの力である、という点である。
力を面積で除して得られる応力は圧力と同じ単位を持ち、通常\(MPa\)(メガパスカル)という単位で表現される。
ひずみとは、「物体に生じる単位長さ当たりの変位量」をいう。
応力の場合と同じく、単位長さ当たりであることが重要である。
変位量すなわち長さを長さで除して得られるひずみは、単位をもたない無次元量である。通常パーセントや小数で表現される。
以下で具体的に見ていこう。
垂直応力と垂直ひずみ
一軸の引張試験で用いられる応力・ひずみについて述べる。
次のような断面積\(S\)の丸棒に対して、軸方向に荷重\(F\)をかけたとする。
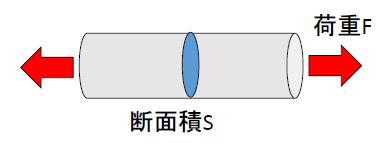
このとき、荷重軸方向に垂直な断面に働く応力\(\sigma\)は次式で与えられる。
このように、ある面の垂直方向に働く応力を垂直応力という。
また、荷重をかけているその瞬間の断面積を用いて計算する応力を真応力という。これに対して、初期の断面積を用いて計算する応力を公称応力という。
このように垂直応力を作用させると、材料は垂直方向に変形する。
変形前の長さが\(L\)だった物体が、\(\Delta L\)だけ伸びて長さが\(l\)になったとする。
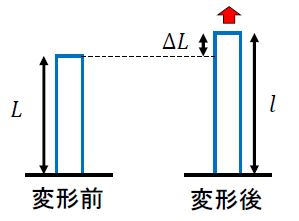
このときの垂直ひずみ\(\varepsilon\)は次式で与えられる。
式からも明らかだが、垂直ひずみは引張変形の場合は正、圧縮変形の場合は負の値となる。
また、ここで求めた垂直ひずみは工学的垂直ひずみともいう。
せん断応力とせん断ひずみ
垂直応力・ひずみは直観的にも理解しやすい。一方、せん断応力・せん断ひずみと呼ばれる量もある。
垂直応力はある面に対して垂直方向に働く応力であった。
これに対して、ある面に平行方向に働く応力をせん断応力といい、\(\tau\)(タウ)で表す。
垂直応力では\(F\)は\(S\)に対し垂直方向だったが、せん断応力では平行方向であることに注意する。
どの面に着目するかで、生じる応力は変化する。例えば、先ほど垂直応力で見た例で、対象とする面を傾けてみよう。
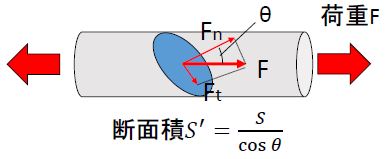
角度\(\theta\)だけ回転した断面に働く応力を計算してみよう。
この面の断面積は\(S^{\prime}=S/\cos\theta\)で与えられる。また、荷重\(F\)を面に垂直な成分\(F_n\)と平行な成分\(F_t\)に分解する。
このとき、垂直応力\(\sigma\)とせん断応力\(\tau\)はそれぞれ次のように計算することができる。
\begin{cases}
\sigma=\displaystyle\frac{F_n}{S^{\prime}}=\frac{F}{S}\cos^2\theta \\
\tau=\displaystyle\frac{F_t}{S^{\prime}}=\frac{F}{S}\sin\theta\cos\theta
\end{cases}
材料に対してせん断応力が作用すると、次のような変形が生じる。
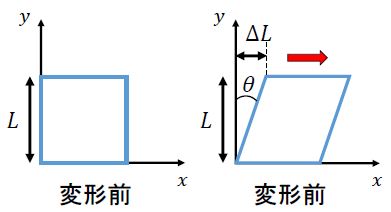
変形前に\(y\)方向長さが\(L\)だった物体が、変形後には\(x\)方向に\(\Delta L\)だけずれたとする。また、図のように角度変化を\(\theta\)とする。
このときのせん断ひずみ\(\gamma\)は次式で与えられる。
さらに、変形が微小であるときは\(\tan\theta≒\theta\)なので、せん断ひずみは角度変化そのものを表すことがわかる。
また、ここで求めたせん断ひずみは工学的せん断ひずみともいう。
公称応力と真応力
垂直応力の部分で軽く触れたが、一軸試験で取り扱う応力には公称応力(nominal stress)と真応力(true stress)がある。
この二つの違いは、どの時点の断面積を用いて計算するかにある。
- 公称応力:\(\sigma_n=\frac{F}{S_0}\) \(S_0\)は初期の断面積
- 真応力:\(\sigma_t=\frac{F}{S}\) \(S\)はそのときの断面積
なぜこんなものがあるのだろうか。それは、次のような事情があるからである。
普通の材料を引っ張ると、変形して断面は次第に小さくなっていく。
初期の断面積は材料試験を行う前に試験片の寸法を測定することで容易に知ることができる。一方で、試験途中の断面積は時々刻々と変化するため、正確に知ることは容易ではない。
試験の結果として得られるのは、ある時刻における荷重と変位であるので、その瞬間の断面積を用いる真応力を直接知ることはできない。
そんなときに用いられるのが、荷重を初期断面積で割って得られる公称応力である。
なお、ある仮定のもとでは公称応力と真応力を変換することが可能である。別記事で解説予定。
公称ひずみと真ひずみ
応力の場合と同様に、ひずみにも公称ひずみ(nominal strain)と真ひずみ(true strain)がある。
この二つの違いも、どの時点を基準にとるかにある。
長さ\(L\)の物体が、引張変形により\(\Delta L\)だけ伸びて長さ\(l\)になったとする。このとき
- 公称ひずみ:\(\varepsilon_n=\displaystyle\frac{l-L}{L}=\frac{\Delta L}{L}\)
- 真ひずみ:\(\varepsilon_t=\displaystyle\int_{L}^{l}\frac{dL^{\prime}}{L^{\prime}}=\ln\left(\frac{l}{L}\right)\)
と計算する。ここで、\(dL^{\prime}\)はある瞬間における変位量を、\(L^{\prime}\)はその直前の長さを表す。
時々刻々と変化するひずみを足し合わせて求められるのが真ひずみである。
自然対数の形で表されるので、対数ひずみ(logarithmic strain)とも呼ぶ。
真ひずみは、①足し合わせが可能、②体積一定条件の取り扱いが容易、といった公称ひずみにはない利点がある。とくに塑性加工を扱う上で頻繁に用いられるためよく理解しておきたい。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]


