塑性変形仕事と加工発熱の計算方法

金属材料を変形させると、熱が発生して材料の温度が上昇する。

これは塑性加工のために必要なエネルギーの大半が熱に変換されるためであり、材料内部で生じる摩擦に起因する。

この記事では、塑性変形におけるエネルギー(仕事)の定義と材料の加工発熱および温度上昇量の計算方法を解説する。

塑性変形仕事

応力の絶対値\(\bar{\sigma}\)と塑性ひずみの絶対値\(\bar{\varepsilon}\)を用いて曲線を描く。

このときの\(\bar{\sigma}\)を変形抵抗ともいい、その曲線を変形抵抗曲線と呼ぶ。

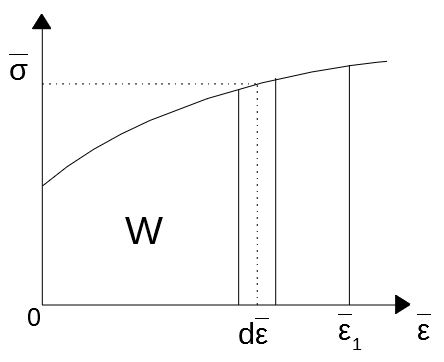
上図のように、応力\(\bar{\sigma}\)の下で微小なひずみ\(d\bar{\varepsilon}\)が生じたとする。

すると、このとき消費される単位体積当たりのエネルギーは\(\bar{\sigma}d\bar{\varepsilon}\)で与えられる。これは外部から与えられた仕事に等しい。

いま、ひずみ0から\(\bar{\varepsilon}_1\)まで塑性変形したとすると、単位体積当たりの全消費エネルギー\(W\)は

で表される。これを塑性変形仕事と呼ぶ。

塑性変形仕事は、変形抵抗曲線の下部の面積に等しい。

加工発熱

塑性加工で消費されるエネルギーの大部分は熱に変換され、材料の温度を上昇させる。これを加工発熱という。

材料の加工発熱は接触工具との熱伝導や大気との熱伝達により拡散する。

加工発熱量は次のように見積もることができる。

簡単のため、変形エネルギーがすべて熱エネルギーに変わる断熱状態を仮定する。

単位体積当たりであることに注意すると、熱量の式から

$$\rho c\Delta T=W$$

よって、材料の温度上昇は

で与えられる。

ただし\(\rho\)は密度\([kg/m^3]\)、\(c\)は比熱\([J/kg・K]\)である。

それでは、簡単な計算問題を解いてみよう。

例題

塑性変形仕事を求めるために、総変形量を対数ひずみで計算する。単位に注意しよう。

(解)

材料の初めの長さを\(l_0\)とすると、この変形で生じたひずみは

\begin{align*}
\bar{\varepsilon}&=\ln\frac{1.2l_0}{l_0}-\ln\frac{l_0}{1.2l_0} \\
&=2\ln1.2
\end{align*}

となる。よって、変形エネルギーは

\begin{align*}
W=\int_{0}^{\bar{\varepsilon}}\bar{\sigma}d\bar{\varepsilon}&=\int_{0}^{2\ln1.2}500\bar{\varepsilon}^{0.25}d\bar{\varepsilon} \\
&=500・\frac{4}{5}\left[\bar{\varepsilon}^{5/4}\right]_{0}^{2\ln1.2} \\
&=113.3 (MJ/m^3)
\end{align*}

したがって、温度上昇\(\Delta T\)は

$$\Delta T=\frac{W}{\rho c}=\frac{113.3×10^6}{461×7800}=31.5 (K)$$

となる。

(解答終)

すべて熱エネルギーになるとすれば、30℃程度の温度変化が発生し得ることが上の計算でわかる。ただし実際には熱エネルギーになるのは90～95%程度と言われており、残りは材料内部にエネルギーとして蓄積される。

実際に金属材料に対して一気に破断するくらいの変形を与えると、手で触れるには熱いくらいの温度になること確かめたことがある。また加工発熱を体験したい人は、針金を何度も曲げて変形させた箇所に触れてみてほしい。（熱いので火傷しないよう気を付けること）

密度と比熱の値は下記サイトより引用した。

各種物質の性質： 金属（固体）の性質（https://www.hakko.co.jp/qa/qakit/html/h01020.htm）

まとめページ

金属工学

金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]