材料力学や構造力学で登場する「はり」について学んでいく。
はりに荷重がかかったときの、任意の断面におけるせん断力や曲げモーメント、変形を計算する。
この記事では、まずはりについて簡単に説明し、はりおよびはりに作用する荷重を分類する。
今後、はりについて論じる際にたびたび登場する基本事項なので、ここで区別して理解しておきたい。
「はり」とは
水平方向に支えられている構造用の棒を、はり(beam)という。
はりの軸線に垂直な方向から荷重を作用させると、せん断力や曲げモーメントが生じてはりが変形する。
例えば下図のように、両端を支えたはりに荷重を加えると、点線のように曲がる。
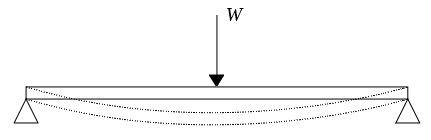
この変形の仕方や変形量については後ほど学んでいく。
荷重を受けないとき、軸線が直線であるものを特に真直はりと呼ぶこともある。以下では単にはりということとする。
荷重
荷重には、一点に集中して作用する集中荷重と、分布して作用する分布荷重がある。
さらに、一様な大きさで分布するものを等分布荷重、不均一なものを不等分布荷重という。
下図に、集中荷重および分布荷重を受けるはりの例を示す。
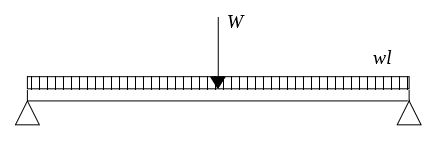
集中荷重は大文字のWで表し、その作用する位置を矢印で示す。
分布荷重は、単位長さのものを小文字のwで表す。
はりの長さをlとするとき、上図のはりに作用する分布荷重はwlで与えられる。
なお、はりには自重があるが、ふつう外部荷重に比べてはりに及ぼす影響が小さいため、特に断りがない限りは無視する。
はりの種類
材料力学で取り扱うはりは、主に以下の4種類である。
- 片持ちはり(cantilever)
- 両端支持はり(simple beam)
- 固定はり(fixed beam)
- 連続はり(continuous beam)
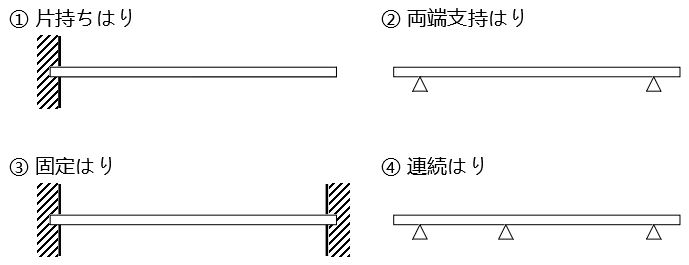
片持ちはりは、はりの一端が固定、他端が自由な状態にあるものをいう。
両端支持はりは、はりの両端が自由に曲がるように支えたものである。特に、はりの片側または両側が支点から外に出ているものを張り出しはり、両端が出ていないものを単純はりという。上の画像は両端張り出しはりである。
固定はりは、はりの両端が固定されたものをいう。
連続はりは、3個以上の支点をもつものをいう。
支点の種類や取り方により、はりに生じる応力や変形が異なる。





