具体的なはりのたわみ計算をしてみよう。
第2回は「両端支持はり」を扱う。
たわみの方程式については前回の記事を参照のこと。
[mathjax] はりに外力が作用すると、はりは変形してたわみが発生する。 ここでは、はりのたわみを表す曲線の方程式を導く。 $$\frac{d^2y}{dx^2}=-\frac{M}{EI_z}$$ たわみ\(y\)と、[…]
両端支持はりのたわみ
集中荷重を受ける両端支持はりを考える。
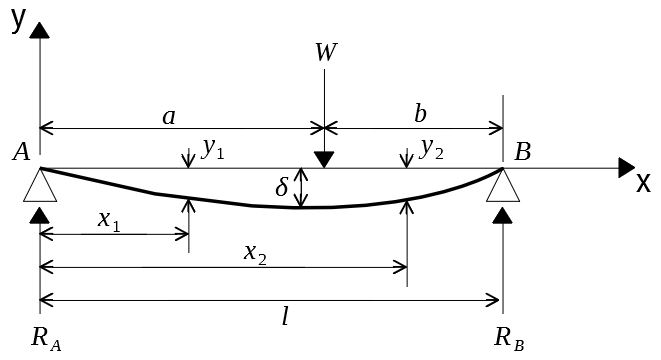
両端支持はり\(AB\)において、\(A,B\)からそれぞれ\(a,b\)の距離にある点\(C\)に集中荷重\(W\)が作用しているとする。
\(AC\)および\(BC\)の部分では、曲げモーメントの分布が異なるので、たわみの方程式も異なる。
よって、\(AC\)部と\(BC\)部に分けて任意の断面\(x_1,x_2\)について考えていく。
たわみ角・たわみの式の導出
\(x_1\)断面のモーメント\(M_1\)は
$$M_1=R_Ax_1=\frac{Wb}{l}x_1$$
\(x_2\)断面のモーメント\(M_2\)は
\begin{align*}
M_2=R_Ax_2-W(x_2-a)&=\frac{Wb}{l}x_2-W(x_2-a) \\
&=\frac{Wa}{l}(l-x_2)
\end{align*}
これより、たわみの方程式は
\begin{cases}
0\le x_1\le aのとき & \displaystyle\frac{d^2y_1}{dx_1^2}=-\frac{Wb}{EI_zl}x_1 \\
a\le x_2\le a+bのとき & \displaystyle\frac{d^2y_2}{dx_2^2}=-\frac{1}{EI_z}\left\{\frac{Wa}{l}(l-x_2)\right\}
\end{cases}
となる。
それぞれ2回積分して、
\begin{cases}
\displaystyle\frac{dy_1}{dx_1}=\displaystyle-\frac{1}{EI_z}\left(\frac{Wb}{l}\frac{x_1^2}{2}+C_1\right) \\
\displaystyle\frac{dy_2}{dx_2}=\displaystyle-\frac{1}{EI_z}\left\{-\frac{Wa}{l}\frac{(l-x_2)^2}{2}+C_1^{\prime}\right\}
\end{cases}
\begin{cases}
y_1=\displaystyle-\frac{1}{EI_z}\left(\frac{Wb}{l}\frac{x_1^3}{6}+C_1x+C_2\right) \\
y_2=\displaystyle-\frac{1}{EI_z}\left\{\frac{Wa}{l}\frac{(l-x_2)^3}{6}-C_1^{\prime}(l-x_2)+C_2^{\prime}\right\}
\end{cases}
ここで、\(C_1,C_2,C_1^{\prime},C_2^{\prime}\)は積分定数で、はりの境界条件により決定される。
まず、\(x_1=0\)で\(y_1=0\)および\(x_2=l\)で\(y_2=0\)であることから
$$C_2=C_2^{\prime}=0$$
である。
次に、\(x_1=x_2=a\)におけるたわみ角およびたわみが等しいことから
$$C_1=-\frac{Wab}{6l}(a+2b),C_1^{\prime}=\frac{Wab}{6l}(2a+b)$$
となる。
これらを代入して、たわみ角およびたわみの式を得る。
\begin{cases}
\displaystyle\frac{dy_1}{dx_1}=\displaystyle-\frac{Wb}{6EI_zl}(3x_1^2-a^2-2ab) \\
\displaystyle\frac{dy_2}{dx_2}=\displaystyle-\frac{Wa}{6EI_zl}\left\{-3(l-x_2)^2+b(2a+b)\right\}
\end{cases}
\begin{cases}
y_1=\displaystyle-\frac{Wb}{6EI_zl}\left\{x_1^3-a(a+2b)x_1\right\} \\
y_2=\displaystyle-\frac{Wa}{6EI_zl}\left\{(l-x_2)^3-b(2a+b)(l-x_2)\right\}
\end{cases}
支点のたわみ角と荷重点のたわみ
支点\(A,B\)におけるたわみ角\(\theta_a,\theta_b\)は、\(x_1=0\)および\(x_2=l\)とおいて
$$\theta_a=\left(\frac{dy_1}{dx_1}\right)_{x_1=0}=\frac{Wab}{6EI_zl}(a+2b)$$
$$\theta_b=\left(\frac{dy_2}{dx_2}\right)_{x_2=l}=-\frac{Wab}{6EI_zl}(2a+b)$$
で与えられる。
また、荷重点\(C\)におけるたわみは、\(x_1=a\)または\(x_2=a\)とおいて
$$y_C=\frac{Wa^2b^2}{3EI_zl}$$
となる。
最大たわみの位置
\(a>b\)のとき、最大たわみは\(dy_1/dx_1=0\)の位置で起こる。すなわち
\begin{align*}
3x_1^2-a^2-2ab&=0 \\
∴x_1&=\displaystyle\sqrt{\frac{a}{3}(a+2b)}
\end{align*}
において
$$(y_1)_{max}=\delta_1=\frac{Wb(l^2-b^2)^{\frac{3}{2}}}{9\sqrt{3}EI_zl}$$
となる。
\(a<b\)のときは\(dy_2/dx_2=0\)として同様に求められる。
$$l-x_2=\sqrt{\frac{1}{3}(l^2-a^2)}$$
$$(y_2)_{max}=\delta_2=\frac{Wa(l^2-a^2)^{\frac{3}{2}}}{9\sqrt{3}EI_zl}$$
中央集中荷重の場合
荷重がはりの中央部に作用している場合、たわみの式に\(a=b=l/2\)を代入する。
\(0\le x\le a\)のとき
$$y_1=-\frac{W}{48EI_z}(4x_1^3-3l^2x_1)$$
であり、最大たわみは\(x_1=l/2\)において
$$\delta=\frac{Wl^3}{48EI_z}$$
となる。





