断面一次モーメント(面積モーメント)につづき、断面二次モーメント(慣性モーメント)について学んでいこう。
[mathjax] はりの曲げや軸のねじり、柱の圧縮などにおいて、曲げにくさやねじりにくさ、座屈しにくさの程度を表す量について述べる。 断面慣性モーメント、断面慣性極モーメント、断面係数などがあり、これらは断面の形状や大きさによ[…]
今後も頻繁に登場する考え方なので、しっかりと理解しておきたい。
断面二次モーメント
断面二次モーメント
とは、曲げに対する抵抗の大きさを表し、形状や大きさによって変化する量である。
断面二次モーメントは以下のように定義される。
\(y^2dA, x^2dA\)を、\(x,y\)軸に関する慣性モーメントという。
これを断面全体について積分したものを、その断面の\(x,y\)軸に関する断面二次モーメントといい
で表す。
断面二次モーメントの性質
を通る軸に関する断面二次モーメントについての性質を紹介する。
図心を\(C\)とし、これを通る軸を\(z\)軸とする。\(z\)軸と平行かつ同一平面上にある軸を\(x\)軸とする。
\(x\)軸に関する断面二次モーメント\(I_x\)と\(z\)軸に関する断面二次モーメント\(I_z\)には
の関係が成り立つ。ここで、\(A\)は断面積、\(y_0\)は軸間の距離である。
(証明)
\(z\)軸から距離\(y\)の位置に微小面積\(dA\)をとる。
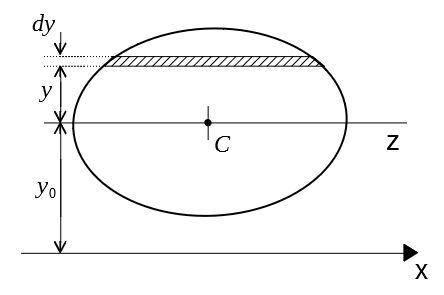
このとき
\begin{align*}
I_x&=\int (y+y_0)^2dA \\
&=\int (y^2+2yy_0+y_0^2)dA \\
&=\int y^2dA+2y_0\int ydA+y_0^2\int dA \\
&=I_z+y_0^2A
\end{align*}
となる。図心を通る軸に関する断面一次モーメントはゼロになることに注意。
(証明終)
長方形断面の例
具体的に断面二次モーメントを求めてみよう。簡単な例として長方形断面を考える。
高さ\(h\)、幅\(b\)の長方形断面において、図心\(C\)を通り、底辺\(x\)軸に平行な軸\(z\)に関する断面二次モーメントを\(I_z\)とする。
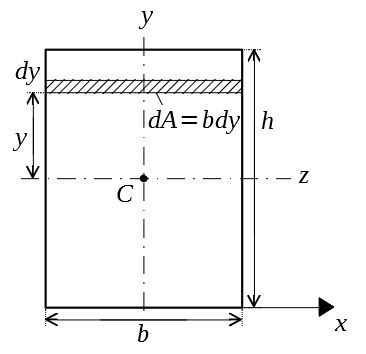
\(z\)軸からの距離が\(y\)の位置に幅\(dy\)の微小帯要素\(dA\)をとると
\begin{align*}
I_z&=\int y^2dA=2\int_{0}^{\frac{h}{2}} y^2bdy \\
&=2b\int_{0}^{\frac{h}{2}} y^2dy=2b・\frac{1}{3}\left(\frac{h}{2}\right)^3 \\
&=\frac{bh^3}{12}
\end{align*}
となる。
同様にして、\(y\)軸に関する断面二次モーメント\(I_y\)は
$$I_y=\frac{hb^3}{12}$$
また、\(x\)軸については上で述べた性質を利用して
$$I_x=I_z+A\left(\frac{h}{2}\right)^2=\frac{bh^3}{3}$$
となる。
断面二次半径
断面二次モーメントから求められる量のひとつに、断面二次半径(回転半径)がある。
後ほど座屈の計算をするときなどに利用するため、ここで定義を述べておく。
断面二次半径\(k\)は、次式で与えられる。
$$k=\sqrt{\frac{I}{A}}$$
\(I\)には具体的に各軸まわりの断面二次モーメントを用いる。
断面係数
断面の図心を通る軸\(z\)に対する断面二次モーメント\(I_z\)を、軸から外周までの距離で割った値を断面係数といい、\(Z\)で表す。
例えば、三角形断面における断面係数は次のように与えられる。
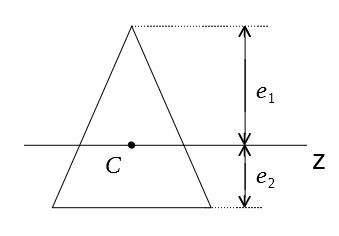
$$Z_1=\frac{I_z}{e_1}, Z_2=\frac{I_z}{e_2}$$





