軸のねじりを起こさせる偶力モーメントを、ねじりモーメントまたはトルクという。
ねじりモーメントによって軸の各断面は互いにずれ、軸断面の中心からの距離に比例したせん断応力(ねじり応力ともいう)が発生する。
断面に生じたせん断応力は軸の周りにモーメントを生じる。このモーメントの総和をねじり抵抗モーメントといい、ねじりモーメントと釣り合う。
ここでは、丸棒のねじりについて解析を行う。
丸棒のねじりの式
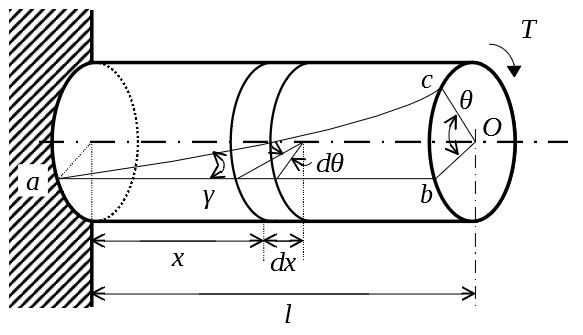
丸棒の一端を固定し、他端には棒の軸線に垂直な面内において偶力\(T\)を加える。
固定端には反作用によって大きさが等しくて逆向きの偶力を生じるから、丸棒は軸線のまわりにねじられてねじり応力が発生する。
以下、ねじりの前後で断面の円形は保たれるとし、ねじれが小さいときは棒の直径および長さは変化しないとする。
棒の表面に軸線と平行に引いた母線\(ab\)は、棒のねじれにより\(ac\)に移動するが、断面半径\(Ob\)は直線のまま\(Oc\)に移動して\(\angle bOc=\theta\)の角をなす。この\(\theta\)をねじれ角という。
\(ac\)を展開すると直線になるので、\(\angle bac=\gamma\)、棒の半径を\(r\)として
$$\tan\gamma=\frac{bc}{ab}=\frac{r\theta}{l}$$
一般に\(\gamma\)は極めて小さいので、
$$\gamma=\frac{r\theta}{l}$$
となる。この\(\gamma\)がねじりモーメントによって長さ\(l\)の丸棒の外周に生じるせん断ひずみである。
次に、棒の一部に長さ\(dx\)の微小円盤を考えると、円盤の左右両断面はねじれた後も平面を保つため、円盤上にとった微小長方形にはせん断応力が生じて平行四辺形に変形する。すなわち、平行四辺形は単純せん断の状態にある。
せん断弾性係数を\(G\)とすると、外周に作用するせん断応力\(\tau\)は
$$\tau=\gamma G=\frac{r\theta}{l}G$$
と表される。このせん断応力は、棒の外周では接線方向と軸線方向とに作用する。
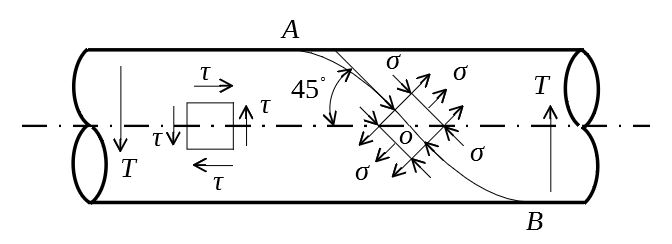
せん断応力\(\tau\)と\(45^{\circ}\)の方向には垂直応力\(\sigma\)が生じ、上図のように引張・圧縮応力が作用する。
この結果、引張に弱い脆性材料をねじった場合、\(AOB\)に沿って破壊が生じる。
ねじり応力\(\tau\)とねじりモーメント\(T\)の関係式を求めよう。
断面の半径\(x\)の位置に幅\(dx\)の微小円環を考えると、次の関係式が成り立つ。
$$\tau_{x}=\frac{x\theta}{l}G$$
この\(\tau_{x}\)の断面中心\(O\)に関する抵抗モーメントの総和は、外部から加えられるねじりモーメントに等しいので、円環の面積を\(dA\)とすると
$$T=\int\tau_{x}・2\pi xdx・x=\int\tau_{x}xdA$$
となる。
せん断応力は中心からの半径に比例するので
$$\tau_{x}=\tau・\frac{x}{r}$$
と表せる。よって
$$T=\frac{\tau}{r}\int x^2dA$$
ここで、\(\int x^2dA\)は中心\(O\)に関する断面二次極モーメント\(I_p\)なので
を得る。これをねじりの式という。
ねじり応力・ねじれ角の計算
上の丸棒について、ねじり応力やねじれ角を計算してみる。
円断面の直径を\(d=2r\)とすると、断面二次極モーメントは
$$I_p=\frac{\pi d^4}{32}$$
である。これをねじりの式に代入して
$$T=\tau\frac{\pi}{16}d^3,\tau=\frac{16T}{\pi d^3}$$
を得る。この式より、丸棒に生じる最大ねじり応力を求めることができる。
次に、ねじりモーメント\(T\)によるねじれ角\(\theta\)を求める。先の図より
$$\gamma=\frac{rd\theta}{dx}$$
$$d\theta=\frac{\gamma}{r}dx=\frac{\tau}{G}\frac{dx}{r}$$
ねじりの式を代入して
$$d\theta=\frac{T}{G}\frac{dx}{I_p}$$
$$\theta=\frac{1}{G}\int_{0}^{l}\frac{T}{I_p}dx$$
\(T\)、\(I_p\)が一定とすると、積分の外に出して
$$\theta=\frac{T}{GI_p}\int_{0}^{l}dx=\frac{Tl}{GI_p}$$
直径\(d\)の丸棒の場合、上の\(I_p\)を代入して
$$\theta=\frac{32Tl}{\pi d^4G}$$
となる。





