この記事では、断面二次極モーメントについて解説する。
これとよく似た量である、断面二次モーメントについてはすでに述べた。
[mathjax] 断面一次モーメント(面積モーメント)につづき、断面二次モーメント(慣性モーメント)について学んでいこう。 [sitecard subtitle=関連記事 url=https://ramenhuhu.com/m[…]
断面二次モーメントは曲げに関する量、断面二次極モーメントはねじりに関する量である。
断面二次極モーメント
断面内の1点\(O\)を通り、その面に垂直な軸に関する慣性モーメントを断面二次極モーメントまたは断面慣性極モーメントといい、\(O\)を極と呼ぶ。
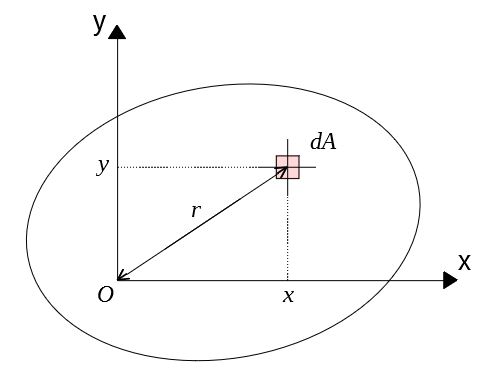
極\(O\)を通り、互いに垂直な軸\(Ox,Oy\)をとる。
断面内の微小面積\(dA\)の座標を\((x,y)\)、\(O\)からの距離を\(r\)とすると、断面二次極モーメントは
となる。
すなわち、慣性極モーメントは、直交する二つの軸に関する慣性モーメントの和に等しい。
計算例
簡単な図形の断面二次極モーメントを求めてみよう。
長方形の断面二次極モーメント
長方形断面の断面二次極モーメントを求める。
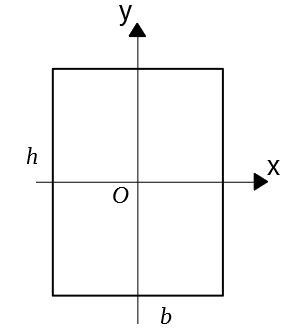
\(x,y\)軸まわりの断面二次モーメントは、それぞれ
$$I_x=\frac{bh^3}{12}$$
$$I_y=\frac{hb^3}{12}$$
であった。
よって、断面二次極モーメントは
$$I_p=I_x+I_y=\frac{bh(h^2+b^2)}{12}$$
となる。
円の断面二次極モーメント
円形断面の断面二次極モーメントを求める。
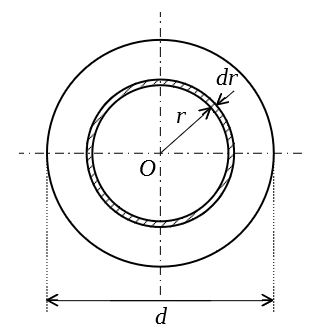
直径\(d\)の円を考える。図のように、半径\(r\)の位置に幅\(dr\)の微小円環をとると、この円環の面積は
$$dA=2\pi rdr$$
で与えられる。よって、断面二次極モーメントは
\begin{align*}
I_p&=\int r^2dA=\int_0^{d/2}r^2・2\pi rdr \\
&=2\pi\int_0^{d/2}r^3dr=2\pi・\frac{1}{4}\left(\frac{d}{2}\right)^4 \\
&=\frac{\pi d^4}{32}
\end{align*}
となる。





