弾性床の上に長いはりをおいたときのたわみを求めよう。
例えば、鉄道の軌条をはりとみなしてモーメントの計算をするときなどに利用することができる。
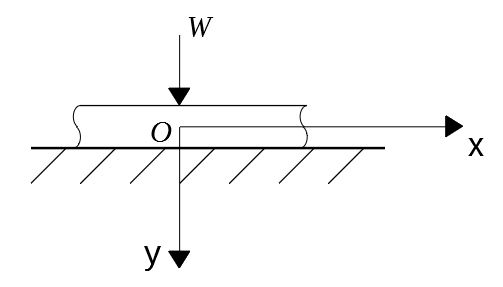
はりのたわみの方程式の導出は以下の記事を参照のこと。
[mathjax] はりに外力が作用すると、はりは変形してたわみが発生する。 ここでは、はりのたわみを表す曲線の方程式を導く。 $$\frac{d^2y}{dx^2}=-\frac{M}{EI_z}$$ たわみ\(y\)と、[…]
$$EI_z\frac{d^2y}{dx^2}=-M$$
の両辺を\(x\)で2回微分する。
$$EI_z\frac{d^4y}{dx^4}=-\frac{d^2M}{dx^2}$$
また、\(\frac{dF}{dx}=-w\)および\(\frac{dM}{dx}=F\)より
$$EI_z\frac{d^4y}{dx^4}-w=0$$
となる。
弾性床がはりに及ぼす反力がたわみに比例して増加する(wi)と仮定する。これを\(py\)で表す。
はりの中央に集中荷重\(W\)が作用しているとき、はりは弾性床から分布荷重
$$w=-py$$
を受ける。よって、はりのたわみの方程式は
$$EI_z\frac{d^4y}{dx^4}+py=0$$
となる。\(p/EI_z=4k^4\)とおいて
$$\frac{d^4y}{dx^4}+4k^4y=0$$
これが解くべき微分方程式である。
\(y=e^{\alpha}\)と仮定して代入すると
$$\alpha^4+4k^4=0$$
$$\alpha=\pm(1\pm i)k$$
となる。これより、微分方程式の一般解は
$$y=e^{kx}(A\cos kx+B\sin kx)+e^{-kx}(C\cos kx+D\sin kx)$$
と表される。ただし\(A,B,C,D\)は任意定数である。
はりのたわみは\(y\)軸に関して対称であるので、\(x\ge0\)について考える。
たわみは荷重点から離れるほど小さくなるので、\(x\to\infty\)のとき\(y\to0\)である。また、\(x=0\)において\(dy/dx=0\)である。
よって、\(A=B=0,C=D\)であり、はりのたわみの式は次式で表される。
$$y=Ce^{-kx}(\cos kx+\sin kx)$$
弾性床がはり全体に及ぼす反力は、はりに作用している集中荷重と等しいので
$$\int_0^{\infty}pydx=\frac{W}{2}$$
となる。これに上で求めた\(y\)を代入して積分すると、定数\(C\)が決定される。
$$C=\frac{Wk}{2p}$$
したがって、はりのたわみの式は
となる。
最大たわみは\(x=0\)で生じ、その値は
$$y_{max}=\frac{Wk}{2p}$$
である。
また、はりの断面に作用する曲げモーメントは
\begin{align*}
M&=-EI_z\frac{d^2y}{dx^2} \\
&=\frac{W}{4k}e^{-kx}(\cos kx-\sin kx)
\end{align*}
となる。





