複素関数の積分で重要なコーシーの積分公式を学ぶ。
コーシーの積分公式
複素関数\(f(z)\)は開集合\(K\)上で正則関数とする。\(C\)を\(K\)に含まれる滑らかな閉曲線とし、\(D\)を\(C\)の内部の領域、\(D^e\)を\(C\)の外部の領域とする。
このとき、次が成り立つ。
$$\frac{1}{2\pi i}\oint_C\frac{f(z)}{z-z_0}dz=f(z_0) (z_0\in D)$$
$$\frac{1}{2\pi i}\oint_C\frac{f(z)}{z-z_0}dz=0 (z_0\in D^e)$$
関数\(f(z)/(z-z_0)\)は、\(z=z_0\)以外の点で正則である。すなわち、点\(z_0\)を内部に含まない周回積分(下式)については、コーシーの積分定理が成り立っている。
上式を、コーシーの積分公式と呼び、正則でない領域を含む周回積分を計算することができる。
定理の証明
関数\(f(z)/(z-z_0)\)は\(z=z_0\)を含まない領域で積分可能である。
点\(z_0\)を含む半径\(\varepsilon\)の円を\(C’\)とすると、コーシーの積分定理より
$$\oint_C\frac{f(z)}{z-z_0}dz=\oint_{C’}\frac{f(z)}{z-z_0}dz$$
が成り立つ。\(C’\)上の点は
$$z=z_0+\varepsilon e^{i\theta} (0\le\theta<2\pi)$$
と書けるので、
$$dz=i\varepsilon e^{i\theta}d\theta$$
である。よって
\[
\begin{align*}
\oint_{C^{\prime}}\frac{f(z)}{z-z_0}dz & =\int_0^{2\pi}\frac{f(z_0+\varepsilon e^{i\theta})}{\varepsilon e^{i\theta}}i\varepsilon e^{i\theta}d\theta \\
& =i\int_0^{2\pi}f(z_0+\varepsilon e^{i\theta})d\theta
\end{align*}
\]
ここで、\(\varepsilon \to 0\)とすると、右辺は\(2\pi i・f(z_0)\)となる。したがって
$$\frac{1}{2\pi i}\oint_C\frac{f(z)}{z-z_0}dz=f(z_0)$$
(証明終)
コーシーの積分公式を使う計算例
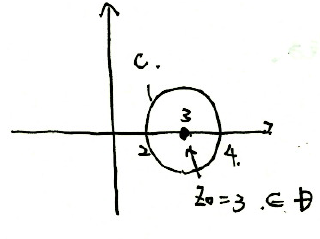
コーシーの積分公式より
$$\frac{1}{2\pi i}\oint_{|z-3|=1}\frac{dz}{z-3}=1$$
$$\oint_{|z-3|=1}\frac{dz}{z-3}=2\pi i$$
$$\frac{8}{(z-1)(z-3)}=\frac{z+1}{z-3}-\frac{z+3}{z-1}$$
と変形する。
\(z=1\)は\(C\)の内部、\(z=3\)は\(C\)の外部にあるので、
\[
\begin{align*}
\oint_{|z|=2}\frac{8}{(z-1)(z-3)} & =\oint_{|z|=2}\frac{z+1}{z-3}dz-\oint_{|z|=2}\frac{z+3}{z-1}dz \\
& =0-2\pi i(1+3) \\
& =-8\pi i
\end{align*}
\]
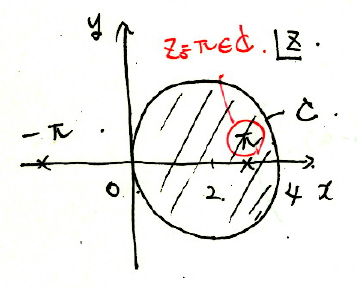
\(z=\pi\)は\(C:|z-2|=2\)の内部、\(z=-\pi\)は\(C\)の外部に存在する。
$$f(z)=\frac{z\cos z}{z+\pi}$$
とみれば、コーシーの積分公式より
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




