前回学んだローラン展開を使うと、特異点を含む周回積分を簡単に計算できる強力な武器を使えるようになる。
ここでは、留数の求め方と留数定理を学んでいく。
留数
関数\(f(z)\)をローラン展開したとき
$$f(z)=\sum_{n=-\infty}^{\infty}c_n(z-a)^n $$
の\(n=-1\)の項の係数を、\(z=a\)における\(f(z)\)の留数(Residue)といい、次のように書く。
$$c_{-1}=\mathrm{Res}_{z=a}f(z)$$
留数の求め方
留数を求めるときは、以下の2通りの方法がある。
(ⅰ)ローラン展開して係数を求める。
(ⅱ)z=aがm位の極であるとき、次の公式により計算することができる。
$$\mathrm{Res}_{z=a}f(z)=\frac{1}{(m-1)!}\lim_{z\to a}\frac{d^{m-1}}{dz^{m-1}}\{(z-a)^mf(z)\}$$
ローラン展開が困難な場合は、この式で計算すればよい。
(導出)
\(z=a\)が\(m\)位の極であるとき、
とかける。この両辺に\((z-a)^m\)をかけると
となる。この両辺を\(m-1\)回微分して\(z=a\)を代入すると、\(c_{-1}\)の項が残る。
$$\lim_{z\to a}\frac{d^{m-1}}{dz^{m-1}}\{(z-a)^mf(z)\}=(m-1)!c_{-1}$$
したがって
留数定理
なぜ留数を求めることが重要なのだろうか。
実は、留数を用いることで周回積分を簡単に計算することができる。これを留数定理と呼び、幅広い分野で応用が利く強力な定理である。
\(f(z)\)は\(C\)上で正則、かつ\(C\)の内部で有限個の孤立特異点\(z_i\)を除いて正則であるとき
$$\oint_Cf(z)dz=2\pi i\sum_{i=1}^{n}\mathrm{Res}_{z=z_i}f(z)$$
特異点を含む領域で周回積分したいときは、留数さえわかれば積分計算をする必要はないということを意味する。
留数定理の証明
留数定理を証明するためには、次の式を導けばよい。
\[
\oint_C(z-z_0)^ndz=\begin{cases}
2\pi i & (n=-1) \\
0& (n \ne -1)
\end{cases}
\]
\(z-z_0=re^{i\theta}\)とおけば、
$$dz=\frac{dz}{d\theta}d\theta=ire^{i\theta}d\theta$$
となる。よって、求めるべき積分は
\[
\begin{align*}
\oint_C(z-z_0)^ndz&=\int_0^{2\pi}\left(re^{i\theta}\right)^n・ire^{i\theta}d\theta \\
& =ir^{n+1}\int_0^{2\pi}e^{i(n+1)\theta}d\theta
\end{align*}
\]
(ⅰ)n=-1のとき
\(n+1=0\)より、
$$i\int_0^{2\pi}d\theta=2\pi i$$
(ⅱ)n≠-1のとき
\[
\begin{align*}
ir^{n+1}\int_0^{2\pi}e^{i(n+1)\theta}d\theta &=ir^{n+1}\int_0^{2\pi}\left[\cos\{(n+1)\theta\}+i\sin\{(n+1)\theta\} \right]d\theta \\
& =\frac{ir^{n+1}}{n+1}\left[\sin\{(n+1)\theta\}-i\cos\{(n+1)\theta\}\right]_0^{2\pi} \\
& =0
\end{align*}
\]
さて、\(f(z)\)を(一つの)特異点\(z_i\)のまわりでローラン展開する。
これを\(C\)に沿って周回積分すると、右辺の積分は\(n=-1\)のときを除いてすべて0である。よって
$$\oint_Cf(z)dz=\oint_C\frac{c_{-1}}{z-z_i}dz=2\pi i\mathrm{Res}_{z=z_i}f(z)$$
複数の特異点を含む場合は、それぞれの特異点について同様の計算をし、足し合わせればよい。
例題
留数の計算と留数定理の使い方を、例題を通じて理解しよう。
$$\oint_{|z|=2}\frac{z^3}{(z+1)(z-1)^3}dz を求めよ。$$
(解)
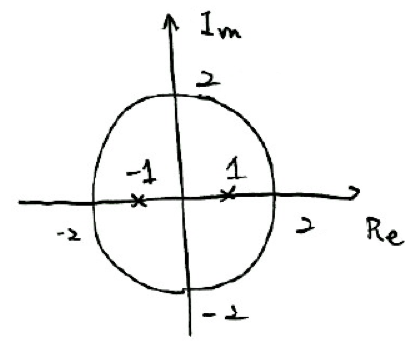
\(z=-1,1\)の2つの特異点を含む周回積分である。まずは留数を求めよう。
\(z=-1\)は1位の極である。よって
\(z=1\)は3位の極なので、
\[
\begin{align*}
\mathrm{Res}_{z=1}f(z) &=\frac{1}{(3-1)!}\lim_{z\to 1}\frac{d^2}{dz^2}\left[(z-1)^3・\frac{z^3}{(z+1)(z-1)^3}\right] \\
& =\frac{1}{2!}\lim_{z\to 1}\frac{2z^3+6z^2+6z}{(z+1)^3} \\
& =\frac{7}{8}
\end{align*}
\]
したがって、留数定理より
\[
\begin{align*}
\oint_{|z|=2}\frac{z^3}{(z+1)(z-1)^3}dz&=2\pi i\left(\frac{1}{8}+\frac{7}{8}\right) \\
& =2\pi i
\end{align*}
\]
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




