複素関数の微分につづき、複素積分の積分を考えていく。
複素平面上にz軸はないので、複素関数の積分は経路Cに沿った線積分を行うことになる。
ベクトル解析の線積分と同様にして複素関数の積分を計算することができる。
複素関数の積分
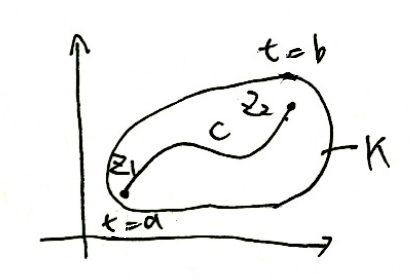
z(t)=x(t)+iy(t)として、C∈Kとする。ただし、Kは単連結な領域である。
$$dz(t)=dx(t)+idy(t)から、\frac{dz}{dt}dt=\left(\frac{dx}{dt}+i\frac{dy}{dt}\right)dt$$
よって、
$$\int_C\frac{df}{dz}dz=f(z_2)-f(z_1)$$
z1=z2(閉曲線)の場合
$$\int_Cf(z)dz\to\oint_Cf(z)dz$$
とかく。このように、閉曲線に沿った線積分を周回積分と呼ぶ。
コーシーの積分定理
f(z)がKで正則関数とする。閉曲線C∈K上の積分について、次が成り立つ。
$$\oint_Cf(z)dz=0$$
この定理は、積分値が積分経路に依存しないことを主張している。すなわち、始点と終点を決めれば積分の値が定まり、その途中経路は任意である。
定理の証明
を思い出しておく。
これを用いて、コーシーの積分定理を証明する。
$$f(z)=u(x, y)+iv(x, y)とする。$$
\[
\begin{align*}
\oint_Cf(z)dz & =\oint_C(u+iv)(dx+idy) \\
& =\oint_C[(udx-vdy)+i(vdx+udy)] \\
& =\iint_D\left[\frac{\partial(-v)}{\partial x}-\frac{\partial u}{\partial y}\right]dxdy+i\iint_D\left[\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right]dxdy \\
& =0
\end{align*}
\]
ただし、f(z)は正則なのでコーシー・リーマンの関係式が成り立つため、[ ]の中身が0になることを用いた。






