実数関数について定義したテイラー展開を、複素関数についても定義していく。
テイラー展開
定義
複素関数\(f(z)\)は、点\(a\)を中心とする半径\(R\)の円およびその内部の領域で正則とする。
このとき、円の内部の点\(z_0\)について、次式が成立する。
$$f(z_0)=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(z_0-a)^n (ただし、|z_0-a|<R)$$
導出
テイラー展開式は実数の場合と同じ形をしているが、複素関数では異なる方法で導出する。
まず、無限等比級数の和の公式を思い出しておこう。
$$1+r+r^2+…=\frac{1}{1-r}$$
これを用いて、次のような式変形を行う。
\[
\begin{align*}
\frac{1}{z-z_0} & =\frac{1}{(z-a)-(z_0-a)} \\
& =\frac{1}{z-a}・\frac{1}{1-\frac{z_0-a}{z-a}} \\
& =\frac{1}{z-a}・\left[1+\left(\frac{z_0-a}{z-a}\right)+\left(\frac{z_0-a}{z-a}\right)^2+…\right] \\
& =\sum_{n=0}^{\infty}\frac{(z_0-a)^n}{(z-a)^{n+1}}
\end{align*}
\]
これを、コーシーの積分公式
に代入すると
\[
\begin{align*}
f(z_0) &=\frac{1}{2\pi i}\oint_C\sum_{n=0}^{\infty}\frac{(z_0-a)^n}{(z-a)^{n+1}}f(z)dz \\
& =\sum_{n=0}^{\infty}\left(\frac{1}{2\pi i}\oint_C\frac{f(z)}{(z-a)^{n+1}}dz\right)・(z_0-a)^n \\
& =\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(z_0-a)^n
\end{align*}
\]
を得る。ただし、最後の式変形にはグルサの定理を用いた。
収束半径
べき級数
の形で表される級数を、べき級数という。
収束半径
このべき級数が、\(|z|<R\)のときに収束し、\(|z|>R\)のときには発散するようなRのことを収束半径という。
収束半径は、以下の式で求められる。
$$R=\lim_{n\to\infty}\frac{|a_n|}{|a_{n+1}|}$$
この極限による収束判定を、ダランベールの収束判定法という。
この定義式に基づいて計算することもできるが、図示すると簡単にわかる場合もある。
複素関数の収束半径は、ある点を中心として正則でない点を含まないような最大の円を描いたときの半径として得られる。
例題
収束半径を2通りの方法で求める。
$$f(z)=\frac{z^2}{(z+2i)(z-2i)}$$
より、点\(z=\pm 2i\)で正則ではない。
\[
\begin{align*}
f(z) &=\frac{z^2}{4}\frac{1}{1+\left(\frac{z^2}{4}\right)} \\
& =\frac{z^2}{4}\frac{1}{1-\left(-\frac{z^2}{4}\right)}
\end{align*}
\]
よって、\(f(z)\)は初項\(\displaystyle \frac{z^2}{4}\)、公比\(\displaystyle -\frac{z^2}{4}\)の無限等比級数の和である。
次にf(z)の第n項について考える。
\[
\begin{align*}
f_n(z) &=\frac{z^2}{4}・\left(\frac{z^2}{4}\right)^{n-1} \\
& =\left(\frac{z}{2}\right)^2・\left[-\left(\frac{z}{2}\right)^2\right]^{n-1} \\
& =(-1)^{n-1}・\left(\frac{z}{2}\right)^{2n} \\
& =(-1)^{n-1}・\left(\frac{1}{2}\right)^{2n}・z^{2n} \\
& =(-1)^{\frac{m}{2}-1}・\left(\frac{1}{2}\right)^{m}・z^{m} (2n=mとおいた)
\end{align*}
\]
よって
と書ける。したがって収束半径\(R\)は
一方、\(f(z)\)を図示すると次のようになる。
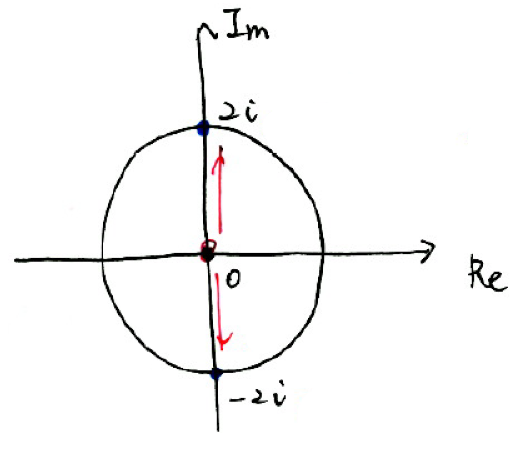
テイラー展開の中心\((z=0)\)から、特異点\((z=\pm 2i)\)を含まない最大の円の半径が収束半径である。よって、\(R=2\)である。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]



