重積分を用いて、体積や曲面の面積を計算することができます。
体積の定式化
空間における体積確定な点集合Vの体積|V|は
$$|V|=\iiint_Vdxdydz$$
で与えられます。
特に、Vが平面\(x=a, x=b (a<b)\)の間にあるとき、
$$|V|=\int_a^b\left(\iint_{V_x}dydz\right)dx=\int_a^b|V_x|dx$$
となります。
すなわち、Vの体積はx軸に垂直な平面によるVの切り口の面積を積分した値に等しくなります。
次に、\(D\)を\(xy\)-平面上の閉領域とし、\(\phi(x, y)、\psi(x, y)\)を\(D\)上の連続関数とします。\(\phi(x, y)\le\psi(x, y)\)とするとき、2つの曲面\(z=\phi(x, y)、z=\psi(x, y)\)で挟まれた立体Vの体積は
$$|V|=\iint_D\{\phi(x,y)-\psi(x,y)\}dxdy$$
となります。
例題 楕円体の体積
$$楕円体 \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\le 1 の体積を求めよ$$
(解)
\(x\)の変域は\(-a\le x\le a\)であり、この\(x\)における切り口は
$$\frac{y^2}{b^2}+\frac{z^2}{c^2}\le 1-\frac{x^2}{a^2}$$
と表される。これは軸の長さが
$$2\sqrt{1-\frac{x^2}{a^2}}b,2\sqrt{1-\frac{x^2}{a^2}}c$$
の楕円である。よって切り口の面積は
$$\pi\left(1-\frac{x^2}{a^2}\right)bc$$
したがって、求める楕円体の体積は
$$\int_{-a}^a\pi\left(1-\frac{x^2}{a^2}\right)bcdx=\frac{4\pi}{3}abc$$
曲面積
\(xy\)-平面上の領域\(D\)で定義された\(C^1\)級の曲面\(S:z=f(x, y)\)を考えます。
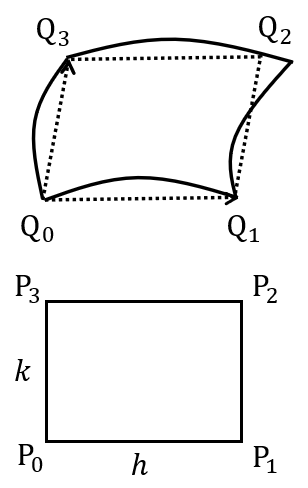
\(D\)内に座標軸に平行な辺をもつ長方形\(P_0P_1P_2P_3\)をとり、\(P_i\)に対応する\(S\)上の点を\(Q_i\)とします。
曲面\(Q_0Q_1Q_2Q_3\)は\(\overrightarrow{Q_0Q_1}、\overrightarrow{Q_0Q_3}\)のつくる平行四辺形に近いものと考え、この面積\(\Delta S\)を求めることにしましょう。
\(P_0(a,b)\),\(P_1(a+h,b)\),\(P_2(a,b+k)\),\(c=f(a,b)\)とし、\(Q_0(a,b,c)\),\(Q_1(a+h,b,c+\delta_1)\),\(Q_2(a,b+k,c+\delta_2)\)とおくと、
\[
\begin{align*}
\Delta S & =\sqrt{\left|\overrightarrow{Q_0Q_1}\right|^2\left|\overrightarrow{Q_0Q_3}\right|^2-\left(\overrightarrow{Q_0Q_1}\cdot\overrightarrow{Q_0Q_3}\right)^2} \\
& =\sqrt{h^2k^2+h^2\delta_2^2+k^2\delta_1^2} \\
\end{align*}
\]
さらに
$$\delta_1=f(a+h,b)-f(a,b)\simeq f_x(a,b)h$$
$$\delta_2=f(a,b+k)-f(a,b)\simeq f_y(a,b)k$$
を用いて、
$$\Delta S\simeq\sqrt{1+f_x^2+f_y^2}(P_0)hk$$
となります。
これより、次の結論を得ます。
\(C^1\)級曲面\(S:z=f(x,y)\)の曲面積\(A\)は次で与えられる。
$$A=\iint_D\sqrt{1+f_x^2+f_y^2}dxdy$$
また、\(D\)が平面の極座標を用いて\(\alpha\le\theta\le\beta、r_1(\theta)\le r_2(\theta)\)と表されるとき
$$A=\int_{\alpha}^{\beta}d\theta\int_{r_1(\theta)}^{r_2(\theta)}\sqrt{1+z_r^2+\frac{1}{r^2}z_{\theta}^2}rdr$$
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]




