重積分の計算方法その2では、変数変換について学びます。1変数のときよりも変換方法が複雑になります。
累次積分法についてはこちら ⇒ 重積分の計算その1
変数変換の準備
置換積分の公式
について考えます。
\(a<b\)とします。\(\phi\)の増加・減少によって\(\alpha\lt \beta\)または\(\beta \lt \alpha\)ですが、いずれの場合についても\(\alpha、\beta\)を両端とする閉区間を\(I\)とすれば\([a, b]=\phi(I)\)なので、上式は
$$\int_{\phi(I)}f(x)dx=\int_If(\phi(t))|\phi'(t)|dt$$
と書き表されます。
区間の拡大率
\(\phi\)を\(C^1\)級とし、\(t=t_0\)を含む微小な閉区間\(e=[t_1, t_2]\)をとると、閉区間\(\phi(e)\)の長さは
$$|\phi(t_2)-\phi(t_1)|=|\phi'(t’_0)||t_2-t_1|,t’_0\in e$$
\(e\)が一点\(t_0\)に縮む、すなわち\(t’_0 \to t_0\)のとき
$$\frac{|\phi(t_2)-\phi(t_1)|}{|t_2-t_1|}=|\phi'(t’_0)|\to|\phi'(t_0)|$$
したがって、\(|\phi'(t’_0)|\)は\(t=t_0\)における微小区間\(e\)と、その像区間\(\phi(e)\)との長さの拡大率と考えることができます。
領域の写像変換
\(\Omega\)を\(uv-\)平面上の領域とし、\(x=\phi(u, v)、y=\psi(u, v)\)は\(\Omega\)上の\(C^1\)級関数とします。
写像\((u, v)\to(x, y)\)は\(\Omega\)を\(xy-\)平面上の領域\(D\)に1対1に写すものとします。
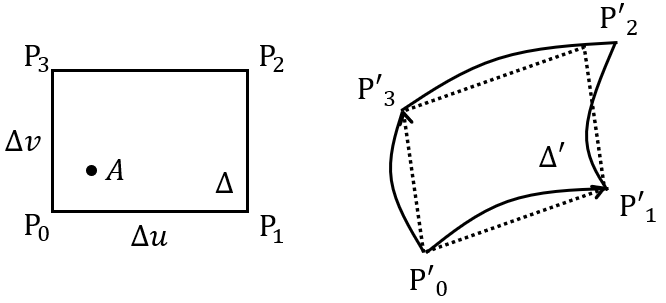
\(\Omega\)内のある点\(A\)を含む微小な長方形\(\Delta:P_0P_1P_2P_3\)をとり、\(P_i\)の像を\(P’_i\)とします。
\(\Delta\)の像\(\Delta’\)は\(P’_0,P’_1,P’_2,P’_3\)を結んだ図形となり、\(\overrightarrow{P’_0P’_1}\)と\(\overrightarrow{P’_0P’_1}\)を隣り合う2辺とする平行四辺形に近い形状となります。
そこで、像\(\Delta’\)の代わりにこの平行四辺形の面積\(\Delta S\)を計算することにします。
$$\overrightarrow{P’_0P’_1}=\left(\phi(P_1)-\phi(P_0),\psi(P_1)-\psi(P_0) \right)$$
$$=\left(\phi_u(P_{01})\Delta u,\psi_u(Q_{01})\Delta u \right)$$
ただし、\(\overrightarrow{P_0P_2}=(\Delta u,\Delta v)\)とし、\(P_{01},Q_{01}\)はともに\(P_0P_1\)上の点とします。
同様にして
$$\overrightarrow{P’_0P’_3}=\left(\phi_v(P_{03})\Delta v,\psi_v(Q_{03})\Delta v \right)$$
よって、
\[
\begin{align*}
\Delta S&=\left|\mathrm{det}\left(\begin{array}{rrr}
\phi_u(P_{01})\Delta u \psi_u(Q_{01})\Delta u\\
\phi_v(P_{03})\Delta v \psi_v(Q_{03})\Delta v
\end{array}\right)\right| \\
&=|\phi_u(P_{01})\psi_v(Q_{03})-\psi_u(Q_{01})\phi_v(P_{03})|\Delta u\Delta v
\end{align*}
\]
\(\Delta\)を1点\(A\)に縮めるとき、\(P_{01},Q_{01},P_{03},Q_{03}\to A\)より
$$\Delta S/\Delta u\Delta v\to|\phi_u(A)\psi_v(A)-\psi_u(A)\phi_v(A)|$$
となります。
関数行列式(ヤコビアン)
一般に、写像\(x=\phi(u,v)、y=\psi(u,v)\)に対して、次の行列式
\[
\mathrm{det}\left(\begin{array}{rrr}
\frac{\partial\phi}{\partial u} & \frac{\partial\phi}{\partial v}\\
\frac{\partial\psi}{\partial u} & \frac{\partial\psi}{\partial v}
\end{array}\right)
\]
$$を \frac{\partial(\phi,\psi)}{\partial(u,v)} または \frac{\partial(x,y)}{\partial(u,v)}$$
とかき、これをこの写像の関数行列式またはヤコビアンと呼ぶ。
重積分の変数変換
さて、ようやく変数変換です。
変数変換\(x=\phi(u, v)、y=\psi(u, v)\)により\(uv-\)平面上の領域\(\Omega\)が\(xy-\)平面上の領域\(D\)の上に1対1に写されるとする。
\(\phi、\psi\)は\(\Omega\)上で\(C^1\)級かつ\(\partial(\phi, \psi)/\partial(u, v)\not =0\)とする。このとき、\(D\)上で広義可積な連続関数\(f(x, y)\)に対して
$$\iint_Df(x,y)dxdy=\iint_{\Omega}f(\phi(u,v),\psi(u,v))\left|\frac{\partial(\phi,\psi)}{\partial(u,v)}\right|dudv$$
が成り立つ。
よく用いられる変数変換の例を挙げておきます。
一次変換:\(x=au+bv,y=cu+dv\)
これは、\(ad-bc\not=0\)のとき、全\(uv-\)平面で1対1の変換です。
\[
\mathrm{det}\left(\begin{array}{rrr}
a&b\\
c&d
\end{array}\right)=ad-bc
\]
より、
$$dxdy=|ad-bc|dudv$$
となります。
極座標変換:\(x=r\cos\theta,y=r\sin\theta(r\gt 0)\)
これは、\(r\theta -\)平面上の領域\(\Omega:0\lt r\lt \infty,0\lt \theta\lt 2\pi\)上で1対1の\(C^{\infty}\)級変換です。
\[
\frac{\partial(x,y)}{\partial(r,\theta)}=\mathrm{det}\left(\begin{array}{rrr}
\cos\theta & -r\sin\theta\\
\sin\theta & r\cos\theta
\end{array}\right)=r
\]
より、
$$dxdy=rdrd\theta$$
となります。
例題
例題を用いて具体的な計算方法について確認していきましょう。
(解)
$$J=\iint_{x,y\ge0}e^{-x^2-y^2}dxdy$$
を考える。\(D_a=\{(x,y)|x^2+y^2\le a^2,x,y\ge0\}\)として
\[
\begin{align*}
J=\lim_{a\to\infty}\iint_{D_a}e^{-x^2-y^2}dxdy & =\lim_{a\to\infty}\int_0^{\frac{\pi}{2}}d\theta\int_0^ae^{-r^2}rdr \\
& =\lim_{a\to\infty}\frac{\pi}{2}\left[-\frac{1}{2}e^{-r^2}\right]_0^a \\
& =\lim_{a\to\infty}\frac{\pi}{4}(1-e^{-a^2}) \\
& =\frac{\pi}{4}
\end{align*}
\]
一方、
$$J=\iint_{0\le x,y\le n}e^{-x^2-y^2}dxdy=\lim_{n\to\infty}\left(\int_0^ne^{-x^2}dx\int_0^ne^{-y^2}dy\right)=I^2$$
である。したがって
$$I=\sqrt{J}=\frac{\sqrt{\pi}}{2}$$
$$I=\iint_{x^2+y^2\le a^2}\sqrt{a^2-x^2-y^2}dxdy(a>0)を計算せよ$$
(解)
\(x=r\cos\theta,y=r\sin\theta\)により変数変換する。
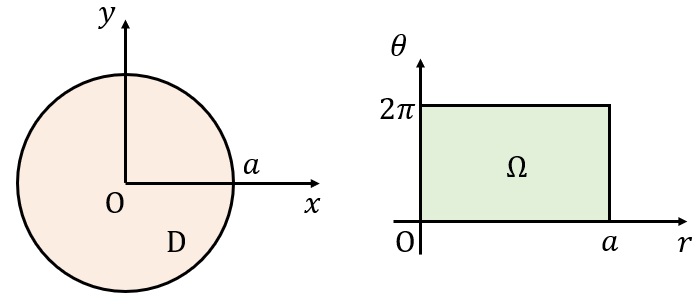
\[
\begin{align*}
I=\iint_D\sqrt{a^2-x^2-y^2}dxdy & =\iint_{\Omega}\sqrt{a^2-r^2}rdrd\theta \\
& =\int_0^{2\pi}d\theta\int_0^a\sqrt{a^2-r^2}rdr \\
& =2\pi\left[-\frac{1}{3}(a^2-r^2)^{\frac{3}{2}}\right]_0^a \\
& =\frac{2\pi}{3}a^3
\end{align*}
\]
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]



