偏微分の応用第3回では、「包絡線」と「全微分方程式」について学んでいきます。
包絡線
あるパラメータ\(\alpha\)を含む方程式\(f(x, y, \alpha)=0\)は、\(\alpha\)を固定すると\(xy\)-平面上で一つの曲線\(C_\alpha\)を表します。
\(\alpha\)を連続的に変化させると、\(C_\alpha\)は連続的に動いて一つの曲線群\(\{C_\alpha\}\)をつくります。
これに対して一つの曲線\(E\)を考えます。
\(E\)が各\(C_\alpha\)と接し、かつ\(E\)の各点が\(C_\alpha\)との接点になっているとき、\(E\)は曲線群\(\{C_\alpha\}\)の包絡線である、といいます。
以下で包絡線の求め方を説明します。
包絡線の方程式
\(E\)が曲線群\(\{C_\alpha\}\)の包絡線であるとします。
\(E\)と\(C_\alpha\)の接点を\(P(\alpha)(x(\alpha), y(\alpha))\)とし、\(x(\alpha)、y(\alpha)\)は微分可能であるとします。
\(P(\alpha)\)において、\(E\)と\(C_\alpha\)の接線が一致するという条件から、次式が成り立ちます。
一方、\(f(x(\alpha), y(\alpha),\alpha)=0\)なので、この両辺を\(\alpha\)で微分して
$$f_\alpha(x(α), y(α),α)$$
以上より、次の定理を得ます。
曲線\(E(x(\alpha), y(\alpha))\)が曲線群\(f(x,y,\alpha)=0\)の包絡線ならば、\(x(\alpha), y(\alpha)\)は
をみたす。
逆に、\(x(\alpha), y(\alpha)\)がこれらを満たし、各曲線が特異点を持たず\((x'(\alpha),y'(\alpha))\not=(0,0)\)ならば
\(x=x(\alpha)、y=y(\alpha)\)
で表される曲線は曲線群\(f(x,y,\alpha)=0\)の包絡線である。
包絡線について例題を使ってイメージしてみましょう。
例題
頂点が\((a,2a)\)の、下に凸な放物線群です。\(a\)を変化させることで、様々な放物線を得ます。
(解)
与式を変形する。
$$f(x,y,a)=(x-a)^2-y+2a=0$$
\(a\)について偏微分して
これを前式に代入して\(a\)を消去すると
$$1^2-y+2(x-1)=0$$
$$y=2x-1$$
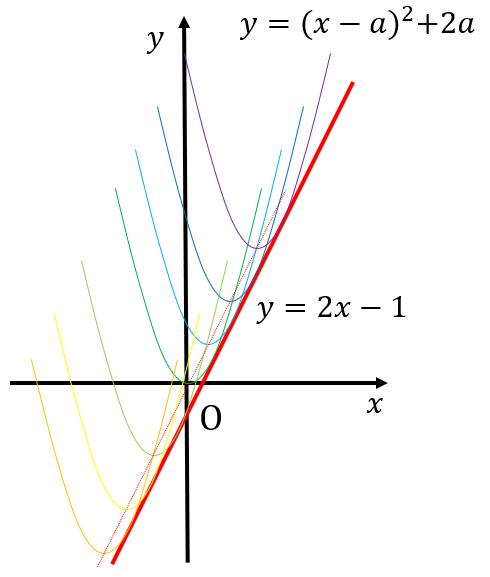
放物線群の頂点が描く軌跡\(y=2x\)と並行な包絡線が引けることがわかりました。
計算の手順をまとめておきます。
①曲線群を表す方程式を\(f(x, y, \alpha)=0\)の形に書き換える
②パラメータ\(\alpha\)で偏微分し、\(\partial f/\partial \alpha=0\)を得る
③二式を連立してパラメータを消去する
全微分方程式
$$P(x,y)dx+Q(x,y)dy=0$$
の形の微分方程式を、全微分方程式という。これは
を書き直したものと考えられる。
これは一般には解けないが、\(C^2\)級関数\(f(x, y)\)が存在して
$$\frac{\partial f}{\partial x}=P,\frac{\partial f}{\partial y}=Q$$
を満たすとき、
$$\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy=df=0$$
となり、\(f(x, y)=c\)は微分方程式の一般解を与える。これを全微分方程式の積分曲線という。
\(\partial f/\partial x=P、\partial f/\partial y=Q\)をみたす\(C^2\)級関数fが存在するとき、元の方程式は完全微分方程式であるという。あるいは左辺を完全微分であるという。
このとき、次式が成り立つ。
$$P_y=Q_x$$
完全性の定理
\(P(x,y)、Q(x,y)\)を\(C^1\)級関数とするとき、全微分方程式
$$Pdx+Qdy=0$$
が完全である条件は、
$$P_y=Q_x$$
が成り立つことである。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]





