ハーゲン・ポアズイユ流れとは
断面積が一定の円管内をゆっくりと流れる
流れを、ハーゲン・ポアズイユ流れという。
ゆっくりした流れではレイノルズ数が小さく、粘性による摩擦力の働きが大きくなる。
ハーゲン・ポアズイユ流れは、ナビエ・ストークス方程式を解析的に解くことができる数少ない厳密解のひとつである。
ナビエ・ストークス方程式の解
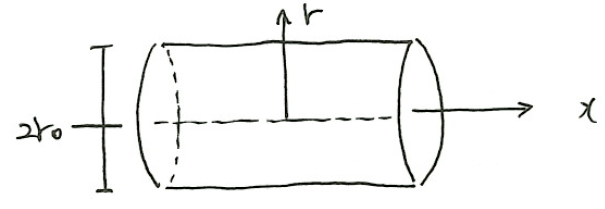
上図のような、断面積一定の円管内を定常流が流れているとする。体積力は無視し、\(v=0\)とする。
円筒座標系のナビエ・ストークス方程式は、次式で与えられた。
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}=F_x-\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu\left(\frac{\partial^2 u}{\partial x^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{\partial^2 u}{\partial r^2}\right)$$
$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial r}=F_r-\frac{1}{\rho}\frac{\partial p}{\partial r}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^2}+\frac{\partial^2 v}{\partial r^2}\right)$$
定常流より時間微分項は0、体積力\(F_x=F_y=0\)、そして\(v=0\)の条件から
\[
\begin{cases}
u\displaystyle{\frac{\partial u}{\partial x}}&=-\displaystyle{\frac{1}{\rho}\frac{\partial p}{\partial x}}+\nu\left(\displaystyle{\frac{\partial^2 u}{\partial x^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{\partial^2 u}{\partial r^2}}\right) \\
0& =-\displaystyle{\frac{1}{\rho}\frac{\partial p}{\partial r}}
\end{cases}
\]
下式より、\(p=p(x)\)となる。
また、\(u\)は\(x\)方向には速度勾配を持たず、\(u=u(r)\)である。よって
$$\frac{\partial u}{\partial x}=\frac{\partial^2 u}{\partial x^2}=0$$
\(\nu=\mu/\rho\)と、偏微分から常微分への書き換えにより上式は
$$\frac{dp}{dx}=\mu\left(\frac{1}{r}\frac{du}{dr}+\frac{d^2u}{dr^2}\right)$$
$$r\frac{dp}{dx}=\mu\frac{d}{dr}\left(r\frac{du}{dr}\right)$$
となる。
両辺を\(r\)で積分して
$$\mu r\frac{du}{dr}=\frac{1}{2}\left(\frac{dp}{dx}\right)r^2+C_1$$
$$\frac{du}{dr}=\frac{1}{2\mu}\left(\frac{dp}{dx}\right)r+\frac{C_1}{\mu}\frac{1}{r}$$
さらに両辺を\(r\)で積分して
$$u=\frac{1}{4\mu}\left(\frac{dp}{dx}\right)r^2+\frac{C_1}{\mu}\ln r+C_2$$
となる。
ここで、\(u\)は有限の値であることから
$$C_1=0 (r\to 0)$$
また、\(r=r_0\)(円管壁面)では\(u=0\)であることから
$$C_2=-\frac{1}{4\mu}\left(\frac{dp}{dx}\right)r_0^2$$
したがって、ハーゲン・ポアズイユ流れの速度は
で与えられる。
流体は圧力が高い方から低い方へ流れるので、\(dp/dx<0\)である。
速度分布
ハーゲン・ポアズイユ流れにおいて、円管半径方向の速度分布を考える。
$$u=-\frac{1}{4\mu}\left(\frac{dp}{dx}\right)(r_0^2-r^2)$$
\(u\)は二次関数になっており、\(r=0\)で最大、\(r=r_0\)で最小値をとる。
\begin{cases}
u_{max}=-\displaystyle{\frac{1}{4\mu}\left(\frac{dp}{dx}\right)}r_0^2 &(管軸) \\
u_{min}=0 &(管壁)
\end{cases}
\]
また、速度比は
$$\frac{u}{u_{max}}=1-\left(\frac{r}{r_0}\right)^2$$
となる。
摩擦応力
半径\(r\)、長さ\(dx\)の微小領域について、力のつり合いを考える。
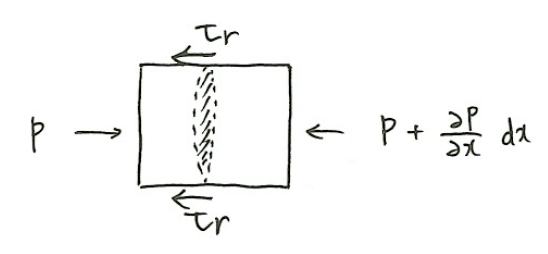
$$-\frac{dp}{dx}\pi r^2dx=\tau_r・2\pi rdx$$
これを整理して、摩擦応力は
流量と平均流速
流量Qは、半径方向に積分して求める。
圧力損失
最後に、管内の圧力損失を与える。
円管の長さLの間の圧力差をΔpとすると、
$$-\frac{dp}{dx}=\frac{\Delta p}{L}$$
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]




