このような流れを、二次元のポアズイユ流れといいます。
(解)
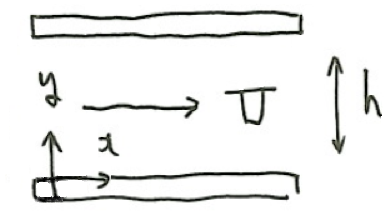
xy-座標系のナビエ・ストークス方程式は
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=F_x-\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right)$$
$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=F_y-\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)$$
で与えられる。
いま、平行流なので\(v=0\)である。定常・非圧縮流れの連続方程式より
$$\frac{\partial u}{\partial x}=0$$
$$u=u(y)$$
である。
これらと体積力=0のもとで、ナビエ・ストークス方程式は
$$0=-\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu\frac{\partial^2 u}{\partial y^2}$$
$$0=-\frac{1}{\rho}\frac{\partial p}{\partial y}$$
となる。下式より、
$$p=p(x)$$
なので、上式は
$$\frac{dp}{dx}=\mu\frac{d^2u}{dy^2}$$
$$∴\frac{d^2u}{dy^2}=\frac{1}{\mu}\frac{dp}{dx}$$
この微分方程式を解けばよい。
両辺をyで2回積分して
境界条件:\(u(0)=u(h)=0\)より、
これは、次のような放物線型の速度分布を表す。

\(y=h/2\)で最大速度\(u_{max}\)をとる。
また、流量については速度を積分して
そして、流量=断面積×流速の関係から平均流速は
せん断応力\(\tau\)は、\(y=h/2\)に対して対称となる。
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]





