オイラーの運動方程式(非粘性流体)
に続き、基礎的な方程式であるオイラーの運動方程式を見ていきましょう。
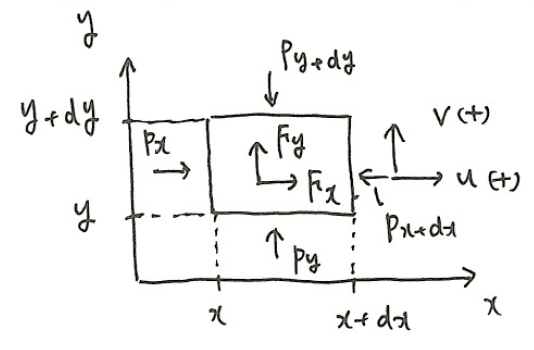
\(xy\)-座標系に一辺が\(dx、dy\)である領域を考える。この領域内の物体に対し、運動方程式を立てたい。
運動方程式を立てるためには、物体に働く力について考えなくてはならない。まず、単位体積当たりの体積力を考える。体積力とは、物体の体積や質量に比例する力のことであり、例えば重力や電磁気力などがある。これを\(F_x、F_y\)とする。
次に、物体の面に働く面積力を考える。面積力とは、物体の面積に比例する力であり、例えば圧力は面積力である。x軸正方向に物体に働く面積力(圧力) は、
\[
\begin{align*}
p_x-p_{x+dx}&=pdy-\left(p+\frac{\partial p}{\partial x}dx\right)dy \\
&=-\frac{\partial p}{\partial x}dxdy
\end{align*}
\]
となる。物体に働く力は、(体積力)+(面積力)で表されるので、x方向について
$$F=mF_x–\frac{\partial p}{\partial x}dxdy$$
質量\(m=\rho dxdy\)であることに注意して
$$\frac{F}{m}=F_x-\frac{1}{\rho}\frac{\partial p}{\partial x}$$
となる。y方向についても同様である。
\(F=ma\)の形でまとめるために、流体の加速度\(a\)について考える。まず、速度\(u=u(x, y, t)\)について
$$du=\frac{\partial u}{\partial x}dx+\frac{\partial u}{\partial y}dy+\frac{\partial u}{\partial t}dt$$
\[
\begin{align*}
\frac{du}{dt}&=\frac{\partial u}{\partial x}・\frac{dx}{dt}+\frac{\partial u}{\partial y}・\frac{dy}{dt}+\frac{\partial u}{\partial t} \\
&=u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\frac{\partial u}{\partial t}
\end{align*}
\]
dv/dtについても同様。(微分について詳細はこちらを参考)
以上より、オイラーの運動方程式が導かれる。
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=F_x-\frac{1}{\rho}\frac{\partial p}{\partial x}$$
$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=F_y-\frac{1}{\rho}\frac{\partial p}{\partial y}$$
粘性流体の場合は、面積力として圧力と摩擦応力を考える必要がある。これはナビエ・ストークスの式と呼ばれ、後ほど導出する。
1次元の流れの場合、\(v=0、F_y=0\)なので
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=F_x-\frac{1}{\rho}\frac{\partial p}{\partial x}$$
さらに、定常流で\(F_x=0\)の場合
$$udu+\frac{dp}{\rho}=0$$
となる。
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=F_x-\frac{1}{\rho}\frac{\partial p}{\partial x}$$
$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=F_y-\frac{1}{\rho}\frac{\partial p}{\partial y}$$
極座標系のオイラーの運動方程式
極座標系におけるオイラーの運動方程式を導出する。
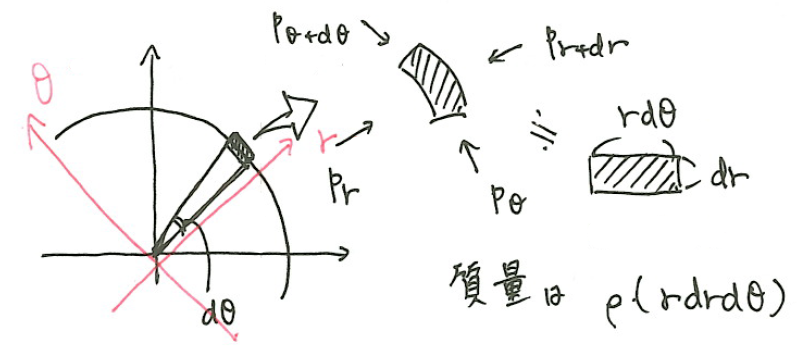
\(r\)方向、\(\theta\)方向について、それぞれ
$$p_r-p_{r+dr}=prd\theta-\left(p+\frac{\partial p}{\partial r}dr\right)rd\theta=-\frac{\partial p}{\partial r}(rdrd\theta)$$
$$p_{\theta}-p_{\theta+d\theta}=pdr-\left(p+\frac{\partial p}{\partial\theta}d\theta\right)dr=-\frac{\partial p}{\partial\theta}(drd\theta)$$
となる。単位質量当たりの体積力を\(F_r、F_{\theta}\)として
\[
\begin{cases}
F_r-\frac{1}{\rho}\frac{\partial p}{\partial r}=a_r &:r方向の加速度 \\
F_{\theta}-\frac{1}{\rho r}\frac{\partial p}{\partial\theta}=a_{\theta} &:θ方向の加速度
\end{cases}
\]
ここで\(r、\theta\)方向の加速度を求めるために座標変換をする。
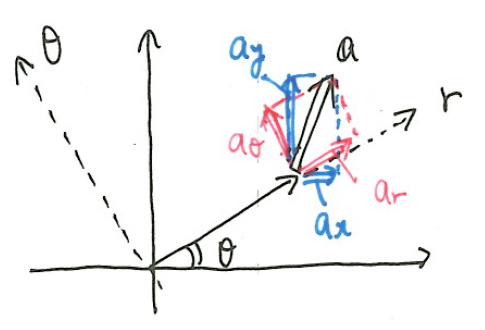
\(r\theta\)平面を\(-\theta\)回転すると\(xy\)-平面に一致することから、
\[
\left[\begin{array}{c}
a_r\\
a_{\theta}
\end{array}\right]
=\left[\begin{array}{rrr}
\cos(-\theta) & -\sin(-\theta)\\
\sin(-\theta) & \cos(-\theta)
\end{array}\right]
\left[\begin{array}{c}
a_x\\
a_y
\end{array}\right]
=\left[\begin{array}{rrr}
\cos\theta & \sin\theta\\
-\sin\theta & \cos\theta
\end{array}\right]
\left[\begin{array}{c}
a_x\\
a_y
\end{array}\right] …(*)
\]
ここで、\(x=r\cos\theta、y=r\sin\theta\)から
$$\dot{x}=\dot{r}\cos\theta-r\sin\theta・\dot{\theta}$$
$$\dot{y}=\dot{r}\sin\theta+r\cos\theta・\dot{\theta}$$
$$a_x=\ddot{x}=\ddot{r}\cos\theta-2\dot{r}\sin\theta・\dot{\theta}-r\cos\theta・(\dot{\theta})^2-r\sin\theta・\ddot{\theta}$$
$$a_y=\ddot{y}=\ddot{r}\sin\theta+2\dot{r}\cos\theta・\dot{\theta}-r\sin\theta・(\dot{\theta})^2+r\cos\theta・\ddot{\theta}$$
(*)式より、\(r\theta\)方向の加速度は
$$a_r=\ddot{r}-r(\dot{\theta})^2=\frac{d^2r}{dt^2}-r\left(\frac{d\theta}{dt}\right)^2$$
さて、\(r\)方向、\(\theta\)方向の速度を\(C_r、C_{\theta}\)とおくと
$$C_r=\frac{dr}{dt} , C_{\theta}=r\frac{d\theta}{dt}$$
と表すことができ、微分の連鎖律より
$$\frac{dC_r}{dt}=\frac{\partial C_r}{\partial r}\frac{dr}{dt}+\frac{\partial C_r}{\partial\theta}\frac{d\theta}{dt}+\frac{\partial C_r}{\partial t}$$
$$\frac{dC_{\theta}}{dt}=\frac{\partial C_{\theta}}{\partial r}\frac{dr}{dt}+\frac{\partial C_{\theta}}{\partial\theta}\frac{d\theta}{dt}+\frac{\partial C_{\theta}}{\partial t}$$
また、
$$a_r=\frac{dC_r}{dt}-r\left(\frac{dC_{\theta}}{dt}\right)^2=\frac{dC_r}{dt}-\frac{{C_{\theta}}^2}{r}$$
以上を整理すると、次式を得る。
$$\frac{\partial C_r}{\partial t}+C_r\frac{\partial C_r}{\partial r}+\frac{C_{\theta}}{r}\frac{\partial C_r}{\partial\theta}-\frac{{C_{\theta}}^2}{r}=F_r-\frac{1}{\rho}\frac{\partial p}{\partial r}$$
$$\frac{\partial C_{\theta}}{\partial t}+C_r\frac{\partial C_{\theta}}{\partial r}+\frac{C_{\theta}}{r}\frac{\partial C_{\theta}}{\partial\theta}+\frac{C_rC_{\theta}}{r}=F_{\theta}-\frac{1}{\rho r}\frac{\partial p}{\partial\theta}$$
以上、かなり大変だったが、オイラーの運動方程式の極座標系を導出することができた。
これを使う演習問題:回転流体の圧力勾配と自由表面形状【流体力学演習】
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]






