これまで、摩擦を無視した理想流体の運動について学んできた。
現実の流体の運動を考える場合、摩擦を考慮して流れの解析を行う必要がある。ここからは、摩擦が働く「粘性流体」の運動を論じていく。
粘性流体の運動
固体壁に沿って流体が流れるとき、壁面と流体の間に働く粘性法則を定式化する。
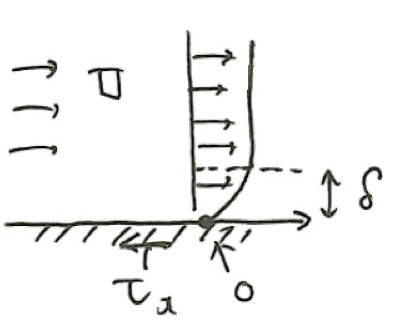
上図のように、速度Uの流体が固体壁に沿って平行に流れているとする。このとき
(ⅰ)固体壁との接点では流体の速度はゼロ
(ⅱ)固体壁との接点で摩擦応力(せん断応力τ)が発生する
摩擦応力は速度勾配に比例して大きくなる。このことを、ニュートンの粘性法則という。
ただし、μは粘性係数、γはせん断ひずみである。
平行流(v=0)においては、
$$\tau=\mu\frac{\partial u}{\partial y}=\mu\frac{du}{dy}$$
(ⅲ)壁面から離れるほど流体の速度は大きくなり、ある距離で元の流速Uと等しくなる
このとき、流速Uで流れる部分を主流、流速が変化する部分を境界層といい、境界層の厚さをδで表すこととする。
ナビエ・ストークスの運動方程式
先に導出したオイラーの運動方程式では、流体に働く摩擦応力を考慮していなかった。
流体の粘性を考慮した運動方程式である、ナビエ・ストークス方程式(Navier-Stokes equations)を導いていく。
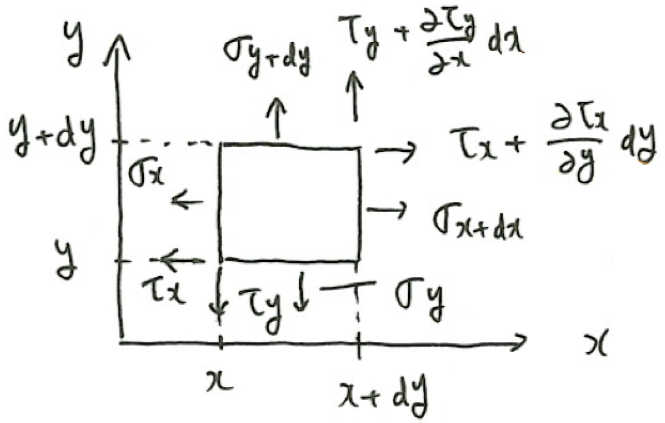
上図のように、流体に働く垂直応力およびせん断応力を考える。
粘性により面積力が増える。例えばx方向に働く面積力は
$$\frac{\partial\sigma_x}{\partial x}dx・dy+\frac{\partial\tau_x}{\partial y}dy・dx$$
とかける。
※応力と圧力は正の向きが異なることに注意。圧力は圧縮方向を正、応力は引張方向を正としている。
これより、オイラーの運動方程式は次のように書き直される。
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=F_x+\frac{1}{\rho}\frac{\partial\sigma_x}{\partial x}+\frac{1}{\rho}\frac{\partial\tau_x}{\partial y}$$
$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=F_y+\frac{1}{\rho}\frac{\partial\sigma_y}{\partial y}+\frac{1}{\rho}\frac{\partial\tau_y}{\partial x}$$
変化したのは、右辺の応力項のみである。
非粘性の場合
$$\tau_x=\tau_y=0 ,\sigma_x=\sigma_y=-p$$
とすれば元のオイラーの方程式を得る。
さらに、応力を成分表示することでナビエ・ストークス方程式を得る。
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=F_x-\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right)$$
$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=F_y-\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)$$
ただし、ν=μ/ρは動粘性係数である。
軸対称円筒座標系のナビエ・ストークス方程式
(r, x)座標系の式を与えておく。
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}=F_x-\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu\left(\frac{\partial^2 u}{\partial x^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{\partial^2 u}{\partial r^2}\right)$$
$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial r}=F_r-\frac{1}{\rho}\frac{\partial p}{\partial r}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^2}+\frac{\partial^2 v}{\partial r^2}\right)$$
管内の流れを解析する際に用いるので、覚えておく。



