ベルヌーイの定理の導出(エネルギー保存則)

流体力学

1 ベルヌーイの定理

ベルヌーイの定理

これで質量保存則・運動方程式・エネルギー保存則の式が出揃い、流体の運動を解析することができるようになる。

オイラーの運動方程式で、y方向働く重力のみ考慮する。

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho}\frac{\partial p}{\partial x}$$

$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-g-\frac{1}{\rho}\frac{\partial p}{\partial y}$$

上式に$dx$、下式に$dy$をかけ、流線の方程式($vdx=udy$)を用いると

\[
(＊)：\begin{cases}
\frac{\partial u}{\partial t}dx+u\frac{\partial u}{\partial x}dx+u\frac{\partial u}{\partial y}dy=-\frac{1}{\rho}\frac{\partial p}{\partial x}dx \\
\frac{\partial v}{\partial t}dy+v\frac{\partial v}{\partial x}dx+v\frac{\partial v}{\partial y}dy=-gdy-\frac{1}{\rho}\frac{\partial p}{\partial y}dy
\end{cases}
\]

となる。ここで、下図のような$s$軸に沿った合速度$U$をとる。

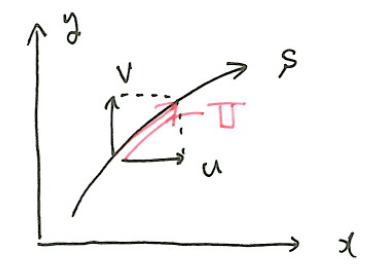
$$U^2=u^2+v^2$$

$s$に関する偏微分について、連鎖律より

$$\frac{\partial}{\partial s}ds=\frac{\partial}{\partial x}dx+\frac{\partial}{\partial y}dy$$

が成り立つので、

$$\frac{\partial u}{\partial x}dx+\frac{\partial u}{\partial y}dy=\frac{\partial u}{\partial s}ds　，　\frac{\partial v}{\partial x}dx+\frac{\partial v}{\partial y}dy=\frac{\partial v}{\partial s}ds$$

$$\frac{\partial p}{\partial x}dx+\frac{\partial p}{\partial y}dy=\frac{\partial p}{\partial s}ds　，　0・dx+g・dy=g・\frac{\partial y}{\partial s}ds$$

(＊)の辺々を足し合わせ、上の関係式を適用すると

$$\left(\frac{\partial u}{\partial t}dx+\frac{\partial v}{\partial t}dy\right)+\left(u\frac{\partial u}{\partial s}ds+v\frac{\partial v}{\partial s}ds\right)=-g\frac{\partial y}{\partial s}ds-\frac{1}{\rho}\frac{\partial p}{\partial s}ds$$

ここで、次の式変形を行う。

\[
\begin{align*}
\frac{\partial u}{\partial t}dx+\frac{\partial v}{\partial t}dy & =\left(\frac{\partial u}{\partial t}\frac{dx}{dt}+\frac{\partial v}{\partial t}\frac{dy}{dt}\right)dt \\
& =\left(u\frac{\partial u}{\partial t}+v\frac{\partial v}{\partial t}\right)dt \\
& =\frac{1}{2}\frac{\partial}{\partial t}(u^2+v^2)dt=\frac{1}{2}\frac{\partial U^2}{\partial t}dt \\
& =\frac{\partial U}{\partial t}Udt=\frac{\partial U}{\partial t}\frac{ds}{dt}dt \\
& =\frac{\partial U}{\partial t}ds
\end{align*}
\]

\[
\begin{align*}
u\frac{\partial u}{\partial s}ds+v\frac{\partial v}{\partial s}ds & =\frac{1}{2}\frac{\partial}{\partial s}(u^2+v^2)ds \\
& =\frac{1}{2}\frac{\partial U^2}{\partial s}ds
\end{align*}
\]

以上より

$$\frac{1}{2}\frac{\partial U^2}{\partial s}+g\frac{\partial y}{\partial s}+\frac{1}{\rho}\frac{\partial p}{\partial s}ds+\frac{\partial U}{\partial t}=0$$

これを$s$について積分して、ベルヌーイの定理を得る。

$$\frac{1}{2}U^2+gy+\int\frac{dp}{\rho}+\int\frac{\partial U}{\partial t}ds=F(t)$$

ただし、$s$は合速度$U$の方向軸である。

定常流の場合

$$\frac{1}{2}U^2+gy+\int\frac{dp}{\rho}=0$$

さらに非圧縮性流体の場合

$$\frac{1}{2}U^2+gy+\frac{p}{\rho}=const$$

となる。

まとめページ

流体力学

流体力学連続方程式(質量保存則)の導出オイラーの運動方程式(直交座標・極座標)の導出流線の方程式と速度ポテンシャル・流れ関数の定義と関係式ベルヌーイの定理(エネルギー保存則)の導出流体の変形と回転・渦度と[…]