はりの曲げや軸のねじり、柱の圧縮などにおいて、曲げにくさやねじりにくさ、座屈しにくさの程度を表す量について述べる。
断面慣性モーメント、断面慣性極モーメント、断面係数などがあり、これらは断面の形状や大きさによって決定される。
まずは断面一次モーメント(面積モーメント)および図心について見ていこう。
断面一次モーメント
断面一次モーメント
は、断面の図心を求めるために用いられる量である。以下でその求め方を解説する。
図のようにxy座標系をとり、その面内に1つの断面形があるとする。
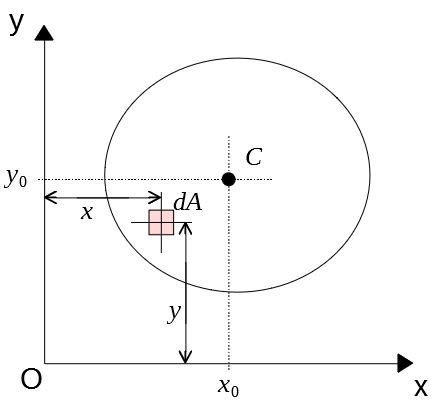
断面内の一点に\((x,y)\)に微小面積\(dA\)をとるとき、\(ydA\)および\(xdA\)をx, y軸に関する断面一次モーメント(または面積モーメント)という。
モーメントという名前がついているが、力のモーメントとは異なる概念であることに注意したい。力のモーメントが「力×距離」であったのに対し、面積モーメントは「面積×距離」で与えられ、単位は\(m^3\)である。
さて、この微小面積を断面内にたくさんとり、それらに対する断面一次モーメントを足し合わせることで、断面全体に対する断面一次モーメントを得ることができる。
x, y軸に関する断面一次モーメントをそれぞれ\(G_x,G_y\)とすると
$$G_x=\int ydA , G_y=\int xdA$$
で与えられる。
長方形断面の例
断面一次モーメント(面積モーメント)の計算例として、長方形断面について考えてみる。
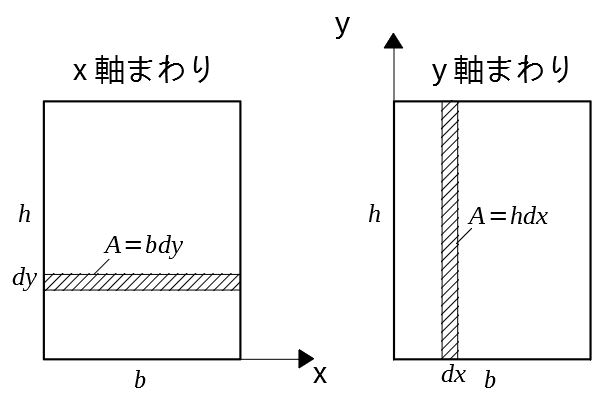
縦\(h\)、横\(b\)の長方形に対し、x,y軸まわりの断面一次モーメントはそれぞれ
$$G_x=\int ydA=\int_0^h ybdy=\frac{bh^2}{2}$$
$$G_y=\int xdA=\int_0^b xhdx=\frac{hb^2}{2}$$
と計算できる。
この結果を利用して、図心の座標を求めることができる。これについては後述する。
面積モーメントがゼロになるような点\(C\)を、その断面の図心と呼ぶ。
図心
図心とは、全面積が一点に集中するような点のことである。
ある基線に関する面積モーメントの合計が、その断面の総面積のその基線に関する面積モーメントに等しい。
図心\(C\)の座標を\((x_0, y_0)\)、断面積を\(A\)とすると
$$A\times x_0=\int xdA, A\times y_0=\int ydA$$
すなわち、図心は面積モーメントおよび断面積から次式で計算することができる。
\(x, y\)両軸に平行で、各軸からの距離がそれぞれ\(x_0,y_0\)である線の交点が図心である。
図心を通る軸に関する面積モーメントはゼロになる。
断面が対称軸を持つ場合、その軸の両側の面積モーメントは打ち消しあうので、対称軸は図心を通る。
複雑な断面形の図心を求めるときは、簡単な図形に分割してそれぞれの面積モーメントを求め、足し合わせて計算することができる。
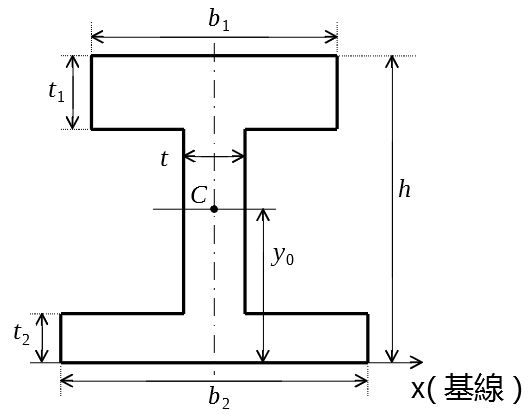
上図のような断面形に対し、図心を求めたい。
下端x軸を基線とする。この断面は対称軸を持つので、図心のx座標は中央の破線を通る。
3つの長方形断面の組み合わせと見なし、各要素の断面一次モーメントを足し合わせればよい。
\begin{align*}
A&=th+t_1(b_1-t)+t_2(b_2)t \\
y_0&=\frac{1}{A}\left\{th・\frac{h}{2}+t_1(b_1-t)\left(h-\frac{t_1}{2}\right)+t_2(b_2-t)・\frac{t_2}{2}\right\}
\end{align*}





