はりの荷重がかかると、荷重と支点反力によってはりにせん断力および曲げモーメントが生じる。
これに対してはりに曲げ応力が生じることで抵抗モーメントが起こり、はりは破壊せずに保たれる。
ここでは、はりの曲げの式
の導出を目指す。
ふつう、曲げに対するせん断力の影響は小さいので、以下では曲げモーメントのみが作用するものとする。
はりの曲げ応力
はりの横断面は図心を通る垂直軸に関して対称とする。また、変形前に平面であった断面は、変形後も平面を保ち、縦断面に垂直であるとする。
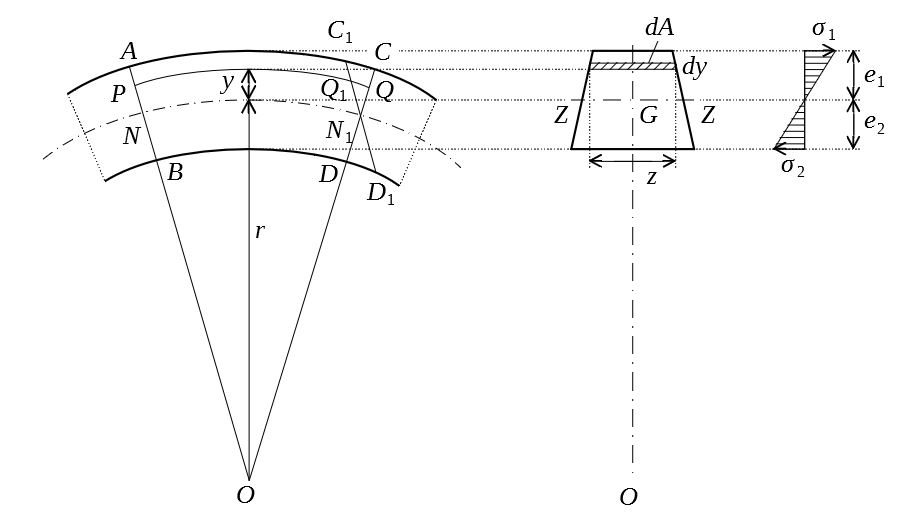
上図は、はりの変形後の横断面および縦断面を示す。
はじめ平行であった2つの断面は、変形後には断面\(AB\)と\(CD\)にように平面のまま傾いて\(O\)で交わる。
図中\(N-N_1\)より上の部分は伸び、下の部分は縮むが、\(N-N_1\)では伸び縮みはない。この\(NN_1\)面を中立面といい、中立面と横断面との交わりを中立軸という。曲げの起こる面と中立面との交わりを、弾性曲線という。
上図でいえば、\(NN_1\)を含み画面に垂直な面が中立面、\(ZZ\)軸が中立軸、\(NN_1\)が弾性曲線である。
断面内の応力・ひずみ分布
\(N_1\)を通り、\(AB\)に平行な線分\(C_1N_1D_1\)を引く。\(AC_1,BD_1\)は、\(AC,BD\)が曲がりを起こす前の長さに等しいので、2つの断面間の曲げによる長さ変化は、伸び側では\(CC_1\)、縮み側では\(DD_1\)となる。また、\(N\)から\(y\)だけ離れた\(PQ\)面においては、\(QQ_1\)だけ長さの変化が生じる。
これらの変形量に対するひずみをそれぞれ\(\varepsilon_1,\varepsilon_2,\varepsilon\)とし、これらに対応する垂直応力をそれぞれ\(\sigma_1,\sigma_2,\sigma\)とすると
$$\varepsilon=\frac{QQ_1}{PQ}=\frac{QQ_1}{NN_1}$$
\(\triangle{Q_1N_1Q}\sim\triangle{NON_1}\)より
$$\frac{QQ_1}{NN_1}=\frac{N_1Q_1}{NO}=\frac{y}{r}$$
ただし、\(r\)は弾性曲線\(NN_1\)の曲率半径を表す。これより
$$\varepsilon=\frac{y}{r}$$
はり材料のヤング率を\(E\)とすれば、フックの法則より
断面\(AB\)に作用する垂直応力は、中立面からの距離\(y\)に比例することがわかる。
はりの上下両面では
$$\varepsilon_{1}=\frac{CC_1}{AC_1}=\frac{CC_1}{NN_1},\varepsilon_{2}=\frac{DD_1}{BD_1}=\frac{DD_1}{NN_1}$$
よって外周応力は、中立軸からの距離をそれぞれ\(e_1,e_2\)とすると
$$\sigma_1=\frac{Ee_1}{r},\sigma_2=\frac{Ee_2}{r}$$
となる。
はりの断面に生じる垂直応力は図に示したように直線的に分布し、外周部で最大引張/圧縮、中立軸上でゼロとなる。
曲げの式
次に、曲げモーメントとはりの曲率半径の関係を導こう。
中立軸\(ZZ\)から距離\(y\)の位置に幅\(dy\)の微小面積\(dA\)をとる。はりは引張や圧縮を受けていないので、垂直応力の断面全体の合計はゼロである。
$$\int\sigma dA=0$$
先に求めた\(\sigma\)を代入すると
$$\int\sigma dA=\int\frac{E}{r}ydA=\frac{E}{r}\int ydA=0$$
$$∴\int ydA=0$$
この式は、中立軸に対する面積モーメントがゼロであることを表す。すなわち、中立軸は図心を通る。
\(dA\)に作用する力\(\sigma dA\)の、中立軸\(ZZ\)に対するモーメントは
$$dM=y\sigma dA=\frac{E}{r}y^2dA$$
である。これを断面全体で足し合わせたものが曲げモーメント\(M\)なので
$$M=\int y\sigma dA=\frac{E}{r}\int y^2dA=\frac{EI_z}{r}$$
したがって
を得る。
はりの曲率\(\frac{1}{r}\)は、曲げモーメント\(M\)に比例し、\(EI_z\)に逆比例する。\(E\)は材料、\(I_z\)は断面形状および寸法に依存する値であり、これらを掛け合わせた\(EI_z\)を曲げこわさ(曲げ剛性)と呼び、曲率に単位変化を生じるために必要な曲げモーメントを表す。
次に、応力と曲げモーメントの関係を導こう。
\(\sigma=\frac{Ey}{r}\)から\(\frac{1}{r}=\frac{\sigma}{Ey}\)である。これを上式に代入して
あるいは、断面係数\(Z=\frac{I_z}{y}\)を用いると
$$M=\sigma\frac{I_z}{M}=\sigma Z$$
となる。
曲げ応力は曲げモーメントに比例するから、最大曲げモーメントが作用する面には最大曲げ応力が生じる。この断面がはりの破損において最も危険であることから、危険断面と呼ぶ。また、\(\sigma Z\)は曲げモーメントに抵抗するはりの応力モーメントを表し、これを抵抗モーメントと呼ぶ。





