ここでは、具体的なはりについてたわみの計算をしてみよう。
第1回は「片持ちはり」を扱う。
たわみの方程式については前回の記事を参照のこと。
[mathjax] はりに外力が作用すると、はりは変形してたわみが発生する。 ここでは、はりのたわみを表す曲線の方程式を導く。 $$\frac{d^2y}{dx^2}=-\frac{M}{EI_z}$$ たわみ\(y\)と、[…]
片持ちはりのたわみ
集中荷重を受ける場合
自由端に集中荷重を受ける片持ちはりを考える。
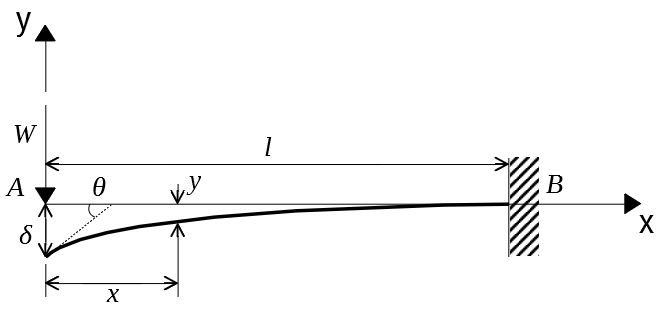
図のように、長さ\(l\)の片持ちはりの自由端\(A\)に集中荷重\(W\)が作用しているとする。
\(A\)から\(x\)の位置の断面に働く曲げモーメントは
$$M=Wx$$
である。ただし、\(y\)軸を下向きにとった場合は負符号になる。
たわみの方程式は
$$\frac{d^2y}{dx^2}=-\frac{M}{EI_z}=-\frac{W}{EI_z}x$$
ここで、\(E\)はヤング率、\(I_z\)は断面二次モーメントである。
上式を\(x\)について積分して
$$\frac{dy}{dx}=-\frac{W}{EI_z}\left(\frac{x^2}{2}+C_1\right)$$
もう一度\(x\)について積分して
$$y=-\frac{W}{EI_z}\left(\frac{x^3}{6}+C_1x+C_2\right)$$
となる。
境界条件:\(x=l\)で\(dy/dx=0\)および\(y=0\)なので
$$C_1=-\frac{l^2}{2},C_2=\frac{l^3}{3}$$
となる。したがって
\begin{align*}
\frac{dy}{dx}&=-\frac{W}{2EI_z}(x^2-l^2)=\frac{W}{2EI_z}(l^2-x^2) \\
y&=-\frac{W}{6EI_z}(x^3-3l^2x+2l^3)
\end{align*}
となる。これがたわみ角およびたわみを与える式である。
最大たわみ角および最大たわみは\(x=0\)の自由端で生じる。
\begin{align*}
\left(\frac{dy}{dx}\right)_{max}&=\theta=\frac{Wl^2}{2EI_z} \\
y_{max}&=\delta=-\frac{Wl^3}{3EI_z}
\end{align*}
等分布荷重を受ける場合
分布荷重の単位長さ当たりの大きさを\(w\)とすると、\(x\)の位置に生じる曲げモーメントは
$$M=wx・\frac{x}{2}=\frac{1}{2}wx^2$$
で与えられる。これは、荷重\(wx\)が\(x\)の部分の中央に集中して作用すると考えればよい。
集中荷重の場合と同様に、たわみの方程式に代入して解けばよい。
$$\frac{d^2y}{dx^2}=-\frac{M}{EI_z}=-\frac{w}{2EI_z}x^2$$
\(x\)について積分して
$$\frac{dy}{dx}=-\frac{w}{2EI_z}\left(\frac{x^3}{3}+C_1\right)$$
$$y=-\frac{w}{2EI_z}\left(\frac{x^4}{12}+C_1x+C_2\right)$$
となる。
\(x=l\)で\(dy/dx=0\)および\(y=0\)なので
$$C_1=-\frac{l^3}{3},C_2=\frac{l^4}{4}$$
となる。したがって
\begin{align*}
\frac{dy}{dx}&=\frac{w}{6EI_z}(l^3-x^3) \\
y&=-\frac{w}{24EI_z}(x^4-4l^3x+3l^4)
\end{align*}
最大たわみ角および最大たわみは\(x=0\)の自由端で生じる。
\begin{align*}
\theta&=\frac{wl^3}{6EI_z} \\
\delta&=-\frac{wl^4}{3EI_z}
\end{align*}





