三角関数や指数関数、対数関数などを多項式の和(級数)の形で表す方法として、テイラー展開またはマクローリン展開があります。
これは前回までに学習したテイラーの定理を利用したものです。
関数の級数展開
「関数を展開する」とは、簡単な多項式を足し合わせることで元の関数の近似値を計算することです。
関数の\(C^n\)級
関数\(f(x)\)が区間\(I\)で\(n\)回微分可能で、\(n\)次導関数が\(I\)で連続であるとき
$$f(x)はI上でC^n級である$$
という。特に、\(f(x)\)が\(I\)上で何度でも微分可能であるとき、\(f(x)\)は\(I\)上\(C^{\infty}\)級であるという。
言葉の定義だけです。例えば、\(f(x)=exp(x)\)は\(I=(-\infty. \infty)\)で何度でも微分可能であり、導関数も連続です。よって、\(f(x)=exp(x)\)は\(C^{\infty}\)級です。
テイラー展開
関数\(f(x)\)が\(x=a\)を内部に含む区間で\(C^{\infty}\)級とすると、次式が成立する。
したがって、\(R_n\to0 (n\to\infty)\)であれば、
となり、\(f(x)\)が\(a_n(x-a)^n\)の形の項の無限級数に展開される。
このときの右辺を、\(f(x)\)の\(x=a\)における「テイラー展開(Taylor series)」と呼ぶ。
マクローリン展開
テイラー展開において、特に\(a=0\)のときは
となる。これを、\(f(x)\)の「マクローリン展開(Maclaurin series)」と呼ぶ。
主な関数のマクローリン展開
公式的に用いられる関数の展開例を挙げます。
$$(1) e^x=1+x+\frac{x^2}{2!}+…+\frac{x^n}{n!}+… (|x|<\infty)$$
$$(2) \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-…+(-1)^n\frac{x^{2n+1}}{(2n+1)!}+… (|x|<\infty)$$
$$(3) \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-…+(-1)^n\frac{x^{2n}}{(2n)!}+… (|x|<\infty)$$
$$(4) \log (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-…+(-1)^{n-1}\frac{x^n}{n}+… (|x|<1)$$
$$(5) (1+x)^\alpha=1+\alpha x+\frac{\alpha (\alpha-1)}{2!}x^2+…+\frac{\alpha (\alpha-1)…(\alpha -n+1)}{n!}x^n+… (|x|<1)$$
上式を使うことで、近似値を計算することができます。
例えば、(1)で\(x=1\)として、\(n=5\)までを計算してみると
$$e=1+1+\frac{1}{2}+\frac{1}{6}+\frac{1}{24}+\frac{1}{120}=2.7166…$$
となり、e=2.71828…との誤差は約0.0016となります。
オイラーの公式の導出
マクローリン展開の式から、かの有名なオイラーの公式を簡単に導出することができます。
\(e^x\)の展開式に形式的に、\(x=i\theta (i=\sqrt{-1})\)を代入すると
\[
\begin{align*}
e^{i\theta}&=1+i\theta-\frac{\theta ^2}{2!}-\frac{i\theta ^3}{3!}+\frac{\theta ^4}{4!}+\frac{i\theta ^5}{5!}-… \\
&=\left(1-\frac{\theta ^2}{2!}+\frac{\theta ^4}{4!}-…)+i(\theta-\frac{\theta ^3}{3!}+\frac{\theta ^5}{5!}-…\right)
\end{align*}
\]
それぞれの( )の中身を三角関数の展開式(2)(3)と比較すると
$$e^{i\theta}=\cos \theta+i\sin \theta$$
指数関数と三角関数をつなぐ重要で美しい関係式です。
追加:cosのグラフ
\(\cos x\)のマクローリン展開式をグラフにすると下のようになります。
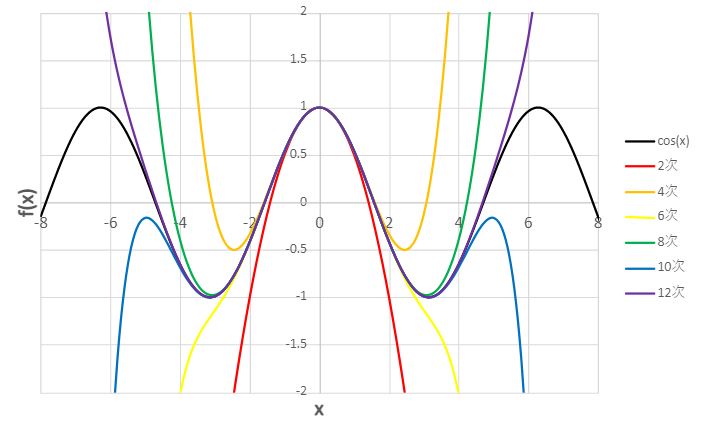
項の数を増やすほど、\(\cos x\)のグラフに近づいていく様子がわかります。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]





