これまでに、線形計画問題の解法として通常のシンプレックス法、罰金法、そして計算機でよく用いられる二段階のシンプレックス法について例題を解きながら学んできた。
この記事では、最後のテーマとして双対シンプレックス法について学ぶ。
双対シンプレックス法
これまで取り扱ってきた問題では、制約条件
\[\begin{cases}
a_{11}x_1 + \cdots + a_{1n}x_n \le b_1 \\
a_{21}x_1 + \cdots + a_{2n}x_n \le b_2 \\
~~~\vdots \\
a_{m1}x_1 + \cdots + a_{mn}x_n \le b_m \\
~~x_1, \cdots, x_n \ge 0
\end{cases}\]
のもとで、目的関数\(z\)の最大化
$$z=c_1x_1 + \cdots + c_nx_n \to max$$
を考えてきた。
これに対し、制約条件
\[\begin{cases}
y_1a_{11} + \cdots + y_ma_{m1} \ge c_1 \\
y_1a_{12} + \cdots + y_ma_{m2} \ge c_2 \\
~~~\vdots \\
y_1a_{n1} + \cdots + y_ma_{mn}x_n \ge c_m \\
~~y_1, \cdots, y_m \ge 0
\end{cases}\]
のもとで、目的関数\(w\)の最小化
$$w=y_1b_1 + \cdots + y_mb_m \to min$$
を考える。
元々の問題のことを線形計画の主問題あるいは表の問題、新たに考えた問題のことを双対線形計画の問題あるいは裏の問題という。
双対シンプレックス法の計算手順を、簡単な例を解きながらみていこう。
双対シンプレックス法の計算手順
\[\begin{align*}
\mathrm{Maximize} & z=6x_1+8x_2 \\
\mathrm{subject~to} & 4x_1+x_2\le20 \\
& x_1+4x_2\le40 \\
& x_1,x_2\ge0
\end{align*}\]
を双対シンプレックス法を用いて解いてみよう。
まず、この問題の双対問題を立てる。
\[\begin{align*}
\mathrm{Minimize} & w=20y_1+40y_2 \\
\mathrm{subject~to} & 4y_1+y_2\ge6 \\
& y_1+4y_2\ge8 \\
& y_1,y_2\ge0
\end{align*}\]
この問題を標準形式に変換する。
制約条件および目的関数に\(-1\)をかけ、スラック変数を導入する。
\[\begin{align*}
\mathrm{Maximize} & w’=-20y_1-40y_2 \\
\mathrm{subject~to} & -4y_1-y_2+\mu_1=-6 \\
& -y_1-4y_2+\mu_2=-8 \\
& y_1,y_2\mu_1,\mu_2\ge0
\end{align*}\]
主問題のスラック変数は\(\lambda\)で表したが、双対問題では\(\mu\)を用いて区別する。同様に、主問題のシンプレックス基準を\(\omega\)で表すのに対し、双対問題のシンプレックス基準は\(\pi\)で表す。
繰り返しのサイクル数を\(h=0\)とし、シンプレックス計算を行う。
STEP1 基底から出す変数を決定する
基底変数のうち、負で絶対値最大のものを選ぶ。
この行を\(k\)列とする。
STEP2 新たな基底変数を決定する(増加限界\(\theta\)の計算)
\(k\)行の要素\(a_{kj}\)が負のものに対し、増加限界\(\theta_j=\pi_j/(-a_{kj})\)を計算する。
そのうち最小の増加限界を持つ列を\(l\)列とする。
STEP3 基底変換を行う
\((k,l)\)要素をピボットとして掃き出し計算を行い、新しいシンプレックス表を作成する。
すべてのc_iが正であればそれが最適解である。そうでなければサイクル数を\(+1\)してSTEP1に戻る。
この手順に基づいて双対問題のシンプレックス・タブローを作成すると、次のようになる。
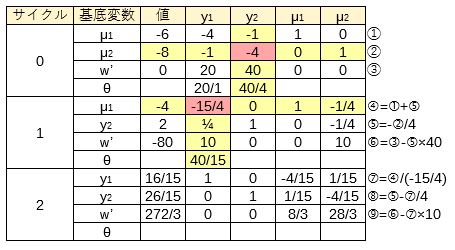
最適解は\(272/3\)である。
なお、主問題のタブローは次のようになる。
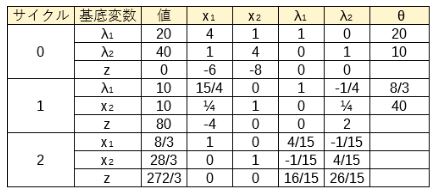
さて、主問題と双対問題の最終タブローを比較してみよう。

次の関係があることがわかる。
- 主問題の解が双対問題のシンプレックス基準\(\boldsymbol{\pi}\)になっている(青)
- 双対問題の解が主問題のシンプレックス基準\(\boldsymbol{\omega}\)になっている(緑)
- 目的関数の値は等しい(オレンジ)
このように、行列が密接な関係を持つ。
線形計画問題では、主問題を解くと同時に双対問題の解が求まっており、その逆も成り立つ。これを双対定理という。
双対定理
一般の線形計画問題
\[\begin{align*}
\mathrm{Maximize} & z=\boldsymbol{c}^{T}\boldsymbol{x} \\
\mathrm{subject~to} & \boldsymbol{A}\boldsymbol{x}\le\boldsymbol{b} \\
& \boldsymbol{x}\ge\boldsymbol{0}
\end{align*}\]
に対して、双対問題を次のように書くことができる。
\[\begin{align*}
\mathrm{Minimize} & w=\boldsymbol{b}^{T}\boldsymbol{y} \\
\mathrm{subject~to} & \boldsymbol{A}^T\boldsymbol{y}\ge\boldsymbol{c} \\
& \boldsymbol{y}\ge\boldsymbol{0}
\end{align*}\]
このとき、どちらか一方が実行可能解を持てば、もう一方も実行可能解を持つ。
主問題の実行可能解を\(\boldsymbol{x}\)、双対問題の実行可能解を\(\boldsymbol{y}\)とすれば、目的関数の値について
$$z=\boldsymbol{c}^{T}\boldsymbol{x}\le\boldsymbol{b}^{T}\boldsymbol{y}=w$$
という関係が成立する。これを弱双対定理という。
さらに、主問題の最適解を\(\boldsymbol{x}^*\)、双対問題の最適解を\(\boldsymbol{y}^*\)とすると
$$\boldsymbol{c}^*\boldsymbol{x}=\boldsymbol{b}^*\boldsymbol{y}$$
という関係が成立する。これを双対定理という。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]





