前回の記事でシンプレックス法について解説した。
[mathjax] この記事では、線形計画法の代表的な解法であるシンプレックス法について解説する。 線形計画法では、ある制約条件の下で目的関数を最大化または最小化することを考える。 高校数学においても、[…]
この中で、等式や不等号が逆向きの場合の制約条件の取り扱いとして罰金法を紹介した。
この記事では、罰金法によるシンプレックス法の問題の解き方を紹介する。
シンプレックス法の手順は以下の通りである。
STEP1 目的変数(ここでは\(z’\))の行の中で最小の要素を持つ列を\(k\)列とする。
STEP2 \(k\)列の要素\(a_{ik}\)が正のものに対し、増加限界\(\theta_i=b_i/a_{ik}\)を計算する。そのうち最小の増加限界を持つ行を\(l\)とする。
STEP3 \((l,k)\)要素をピボットとして掃き出し計算を行い、新しいシンプレックス表を作成する。
サイクル数を\(+1\)してSTEP1に戻る。
罰金法の例題
次の線形計画問題を、シンプレックス法を用いて解け。
\[\begin{align*}
\mathrm{Minimize} & z=x_1-4x_2+8x_3-7x_4 \\
\mathrm{subject~to} & x_1-x_2-2x_4=5 \\
& 2x_2-3x_3+x_4\le3 \\
& 2x_2-5x_3+6x_4\le5 \\
& x_j\ge0 (j=1,2,3,4)
\end{align*}\]
最小化問題になっているため、\(z’=-z\)の最大化問題に書き換える。
また一つ目の制約条件が等式なので、罰金法を用いて解く。
(解)
等式条件を含むため、罰金法を用いる。
与えられた問題を標準形式に書き換えると、以下のようになる。
\[\begin{align*}
\mathrm{Maximize} & z’=-x_1+4x_2-8x_3+7x_4-M\nu_1 \\
\mathrm{subject~to} & x_1-x_2-2x_4+\nu_1=5 \\
& 2x_2-3x_3+x_4+\lambda_2=3 \\
& 2x_2-5x_3+6x_4+\lambda_3=5 \\
& x_j\ge0 (j=1,2,3,4),\nu_1,\lambda_2,\lambda_3\ge0,
\end{align*}\]
あとは通常のシンプレックス計算を行えばよい。
シンプレックスタブローは以下の通り。
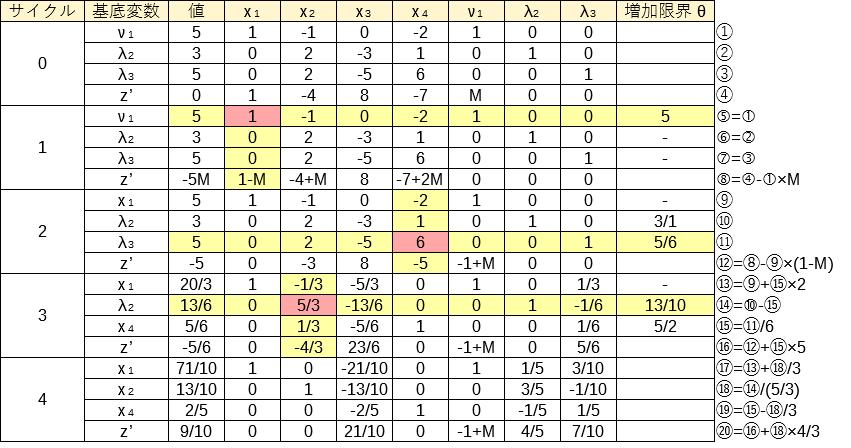
したがって、\(x_1=71/10,x_2=13/10,x_3=0,x_4=2/5\)のとき、最小値\(z=-9/10\)となる。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




