この記事では、線形計画法の代表的な解法であるシンプレックス法について解説する。
線形計画法では、ある制約条件の下で目的関数を最大化または最小化することを考える。
高校数学においても、領域の分野で関数の最大化や最小化という形式で線形計画法の問題が出題されることもある。このときは制約条件を図示し、目的関数を変化させて交点や接点から求めたことを覚えているかもしれない。
しかし変数の数が増えると図示することは不可能になる。そこで、与えられた条件からシステマティックに最適化を行うことができる手法として開発されたのがシンプレックス法である。
ここでは、シンプレックス法の計算手順を説明した後、例題を用いて問題を解く流れを理解することを目標とする。
シンプレックス法
線形計画法の問題は一般に次のように表される。
制約条件:
\[\begin{cases}
a_{11}x_1 + \cdots + a_{1n}x_n \le b_1 \\
a_{21}x_1 + \cdots + a_{2n}x_n \le b_2 \\
~~~\vdots \\
a_{m1}x_1 + \cdots + a_{mn}x_n \le b_m \\
~~x_1, \cdots, x_n \ge 0
\end{cases}\]
目的関数:
$$z=c_1x_1 + \cdots + c_nx_n \to max$$
ここでは目的関数の最大化としているが、最小化問題の場合には-1を掛ければ等価である。
この線形問題を解くためには、次のようにすればよい。
スラック変数と標準形
まず、不等式で与えられた制約条件式に新たな変数を導入し、等式条件に変換する。
\[\begin{cases}
a_{11}x_1 + \cdots + a_{1n}x_n + \lambda_1 &= b_1 \\
a_{21}x_1 + \cdots + a_{2n}x_n + \lambda_2 &= b_2 \\
~~~\vdots \\
a_{m1}x_1 + \cdots + a_{mn}x_n + \lambda_m &= b_m \\
~~x_1, \cdots, x_n, \lambda_1, \cdots, \lambda_m \ge 0
\end{cases}\]
目的関数は
$$z=c_1x_1 + \cdots + c_nx_n + 0・\lambda_1 + \cdots + 0・\lambda_m \to max$$
となる。
ここで導入した\(\lambda_1,\cdots,\lambda_m\)をスラック変数といい、変換されてできた問題を標準形という。
シンプレックス表
標準形の方程式の係数を用いて、以下のようなシンプレックス表(シンプレックス・タブロー)を作成する。

上のシンプレックス表は繰り返し計算を行う前の状態を表すので、サイクル数は\(h=0\)とする。
基底変数とは、0でない値を持つ変数のことをいう。一方、値が0であるとした変数のことを非基底変数という。
はじめは、スラック変数\(\lambda_1,\cdots,\lambda_m\)が定数\(b_1,\cdots,b_m\)に等しい、すなわち変数\(x_1,\cdots,x_n\)は0であるとする。よって、目的変数\(z\)も0である。
STEP1 シンプレックス判定を行う
目的変数\(z\)の行の中で最小の要素を持つ列を\(k\)列とする。
これは非基底変数が1だけ増加したときの目的関数の増分を表し、シンプレックス基準という。すべての基準が非負であるとき、目的変数の値はこれ以上増加しないため、このときの解が最適解であり計算を終了する。
STEP2 新たな基底変数を決定する(増加限界\(\theta\)の計算)
\(k\)列の要素\(a_{ik}\)が正のものに対し、増加限界\(\theta_i=b_i/a_{ik}\)を計算する。
そのうち最小の増加限界を持つ行を\(l\)とする。
STEP3 基底変換を行う
\((l,k)\)要素をピボットとして掃き出し計算を行い、新しいシンプレックス表を作成する。
サイクル数を\(+1\)してSTEP1に戻る。
サイクル数を上付きで表すことにする。新しい要素の計算は以下の通り。
\[\begin{cases}
b_l^{(h+1)} = b_l^{(h)}/a_{lk}^{(h)} \\
b_i^{(h+1)} = b_i^{(h)}-\left(b_l^{(h)}/a_{lk}^{(h)}\right)a_{ik}^{(h)} \\
a_{kj}^{(h+1)} = a_{li}^{(h)}/a_{lk}^{(h)} \\
a_{ij}^{(h+1)} = a_{ij}^{(h)}-\left(a_{li}^{(h)}/a_{lk}^{(h)}\right)a_{ik}^{(h)}
\end{cases}\]
以上がシンプレックス法による計算手順であるが、一般形式ではわかりにくい。
例題を用いて具体的に計算をしながらこの手順を理解していこう。
例題
次の線形計画問題を、シンプレックス法を用いて解け。
\[\begin{align*}
\mathrm{Maximize} & 4x_1+5x_2 \\
\mathrm{subject~to} & 2x_1+5x_2\le20 \\
& 6x_1+4x_2\le27 \\
& 3x_1+x_2\le12 \\
& x_1,x_2\ge0
\end{align*}\]
(解)
まず、スラック変数を用いて制約条件を等式に変換する。この問題の標準形は
\[\begin{align*}
\mathrm{Maximize} & z=4x_1+5x_2+0・\lambda_1+0・\lambda_2+0・\lambda_3 \\
\mathrm{subject~to} & 2x_1+5x_2+\lambda_1=20 \\
& 6x_1+4x_2+\lambda_2=27 \\
& 3x_1+x_2+\lambda_3=12 \\
& x_1,x_2,\lambda_1,\lambda_2,\lambda_3\ge0
\end{align*}\]
となる。
これより、サイクル0のシンプレックス表は次のようになる。
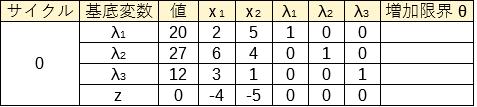
目的関数の行の中で最小の要素は、\(2\)列目の\(-5\)である。次に増加限界を計算すると、最小の値となるのは\(1\)行目の\(20/5=4\)である。
よって\((1,2)\)要素を基準に掃き出し計算を行い、サイクル1に進む。
このようにしてシンプレックス表の更新を繰り返した結果は次のようになる。
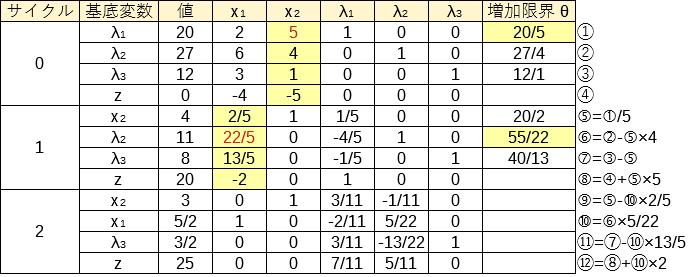
各サイクルで掃き出し計算の基準になる要素を赤文字で示している。また、表の右側に計算内容を記載した。
サイクル2において、シンプレックス基準はすべて非負になっているため、計算は終了となる。
したがって、最適解は\(x_1=5/2,~x_2=3\)のとき\(z=25\)である。
制約条件の取り扱い
上の例で扱った制約条件
$$a_{11}x_1 + \cdots + a_{1n}x_n \le b_1$$
以外の場合の取り扱いについて考えよう。
等式の制約条件の場合
等式の条件式
$$a_{11}x_1 + \cdots + a_{1n}x_n = b_1$$
がある場合は以下のように書き換えればよい。
技巧変数(artificial variable)\(\nu_1\)を導入して
$$a_{11}x_1 + \cdots + a_{1n}x_n + \nu_1 = b_1$$
とする。目的関数は、正で限りなく大きい数\(M\)を用いて
$$z=c_1x_ 1+ \cdots + c_nx_n – M\nu_1 \to max$$
のように与える。
このとき目的関数を最大化するためには、最終的に\(\nu_1=0\)でなくてはならないため、はじめの等式制約条件が満たされることになる。
ここで考えた係数\(M\)のことを罰金と呼び、このようにして行うシンプレックス計算のことを罰金法と呼ぶ。
不等号が逆向きの場合
$$a_{11}x_1 + \cdots + a_{1n}x_n \ge b_1 (b_1\gt0)$$
の場合は、両辺に\(-1\)を乗じて
$$-a_{11}x_1 – \cdots – a_{1n}x_n \le -b_1$$
とする。これを等式条件に直すためにスラック変数を導入する。
$$-a_{11}x_1 – \cdots – a_{1n}x_n + \lambda_1 = -b_1$$
このとき、初めの基底解が\(\lambda_1=-b_1\)で与えられることになるが、これは\(\lambda_1\ge0\)に反する。
そこで、さらに技巧変数を導入し、両辺に\(-1\)を乗じると
$$a_{11}x_1 + \cdots + a_{1n}x_n – \lambda_1 + \nu_1 = b_1$$
となる。このときの初めの基底解は\(\nu_1=b_1\)である。これを制約条件として用いる。
目的変数については、スラック変数の係数は0、技巧変数の係数は\(-M\)として
$$z=c_1x_1 + \cdots + c_nx_n + 0・\lambda_1 – M\nu_1 \to max$$
となる。
\(b_i\)が負の場合
たとえば
$$a_{11}x_1 + \cdots + a_{1n}x_n \le b_1 (b_1\lt0)$$
のとき、両辺に\(-1\)を乗じると上の場合と同じ形になる。
よって、スラック変数と技巧変数を用いて
$$-a_{11}x_1 – \cdots – a_{1n}x_n – \lambda_1 + \nu_1 = -b_1$$
とすることができ、目的関数は
$$z=c_1x_1 + \cdots + c_nx_n + 0・\lambda_1 – M\nu_1 \to max$$
となる。
変数に符号の制約がない場合
変数\(x_i\)に符号の制約がないとき、新しい変数\(x_i^{\prime},x_i^{\prime\prime}\)を導入する。
$$x_i^{\prime}\ge0, x_i^{\prime\prime}\ge0$$
$$x_i=x_i^{\prime}-x_i^{\prime\prime}$$
このように表し、\(x_i^{\prime},x_i^{\prime\prime}\)について解く。
このように、様々な技巧を凝らして計算を行うことが可能であるが、コンピュータを用いて線形計画問題を解く場合は2段階のシンプレックス法と呼ばれる手法が用いられることが多い。
2段階のシンプレックス法については別の記事で解説する。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]





