ある目的関数を最大化または最小化する問題を最適化問題といい、変数が取りうる値に制約がある場合、それを制約条件という。
制約条件と目的関数がともに線形である場合を線形計画問題といい、シンプレックス法という手法を用いて最適解を得る方法について先に解説した。
[mathjax] この記事では、線形計画法の代表的な解法であるシンプレックス法について解説する。 線形計画法では、ある制約条件の下で目的関数を最大化または最小化することを考える。 高校数学においても、[…]
ここからは、目的関数や制約条件が非線形な関数で与えられる、非線形計画問題について考えていきたい。
非線形計画問題とは
目的関数あるいは制約条件が非線形な形で表現される数理計画問題を、非線形計画問題という。
非線形計画問題は、一般に次のように表される。
\[\begin{align*}
目的関数 & f(\boldsymbol{x})\to \min \\
制約条件 & \boldsymbol{x}\in S
\end{align*}\]
ただし、\(\boldsymbol{x}=(x_1,x_2,\ldots,x_n)^T\)であり、\(f：\mathbb{R}^n\to\mathbb{R}，S\in\mathbb{R}^n\)である。
この\(S\)を実行可能領域という。
非線形計画問題を解くための汎用的な方法はなく、問題の性質ごとに適した手法を用いて解く必要がある。
制約条件の有無や性質により、非線形計画問題を分類することができる。
無制約最適化問題
制約条件がなく、単に非線形な目的関数を最適化する問題である。
$$f(\boldsymbol{x})\to \min$$
簡単な例でいえば、二次関数の最小値を求めるような問題はこれに該当する。
有制約最適化問題
一般の最適化問題では、ある制約条件の下で目的関数の最適化を図る。
簡単な例を挙げてみよう。面積が1の四角形のうち、周の長さを最小化する問題は次のように定式化することができる。
\[\begin{align*}
目的関数 & f(x_1,x_2)=2x_1+2x_2\to \min \\
制約条件 & \boldsymbol{x}\in S
\end{align*}\]
制約条件が等式か不等式かあるいは混合か、また条件式は一つなのか複数なのかなど様々なパターンが存在する。
大域的最適解と局所的最適解
次のような最小化問題を考える。
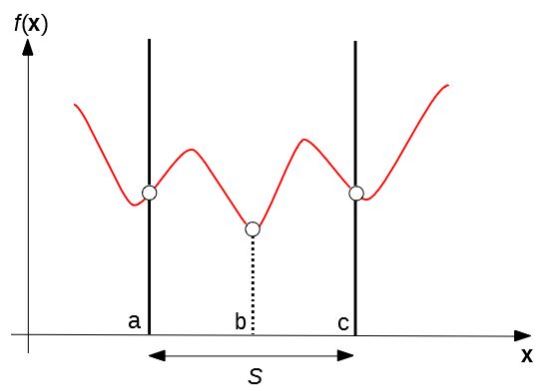
実行可能領域\(S\)の中で、\(x=b\)のとき\(f(x)\)は最小になる。
このような解のことを大域的最適解という。
一方、\(x=a,c\)について、これらの近傍では目的関数は最小値を取っている。
このように、\(x\)の周りでは最適解のような振る舞いをする解のことを局所的最適解という。
局所的最適解は複数ある場合もある。また大域的最適解は局所的最適解のひとつである。
非線形計画問題において、局所解が複数存在するような場合にいかに大域的解を見つけるかが難しいポイントの一つである。
凸計画問題
非線形計画問題の中でも解きやすいものが凸計画問題である。
凸計画問題は、制約領域\(S\)が凸集合かつ目的関数\(f(\boldsymbol{x})\)が凸関数であり、局所的最適解と大域的最適解が等しいという特徴をもつ。
凸集合とは
集合\(S\)が凸集合であるとは、領域に穴や凹みがない状態をいう。
数式を用いると次のように表現できる。
任意の\(\boldsymbol{x},\boldsymbol{y}\in S\)と\(0\le\alpha\le1\)なる\(\alpha\)に対し、\(\alpha\boldsymbol{x}+(1-\alpha)\boldsymbol{y}\in S\)が成立する。
これは次のように図示することができる。
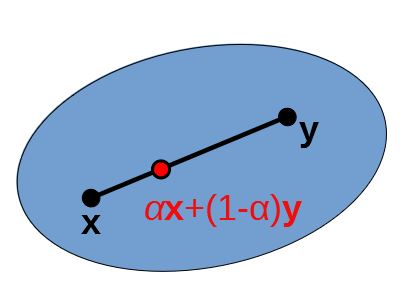\(\alpha\boldsymbol{x}+(1-\alpha)\boldsymbol{y}\)は\(\boldsymbol{x}\)と\(\boldsymbol{y}\)を結ぶ線分上の点を表しており、これがすべて\(S\)に含まれているということは凹みがないことを意味している。
凸関数とは
関数\(f\)が凸関数であることは、次のように表現される。
任意の\(\boldsymbol{x},\boldsymbol{y}\in \mathbb{R}^n\)と\(0\le\alpha\le1\)なる\(\alpha\)に対し、\(f(\alpha\boldsymbol{x}+(1-\alpha)\boldsymbol{y})\le\alpha f(\boldsymbol{x})+(1-\alpha f(\boldsymbol{y}))\)が成立する。
これを図示すると次のようになる。
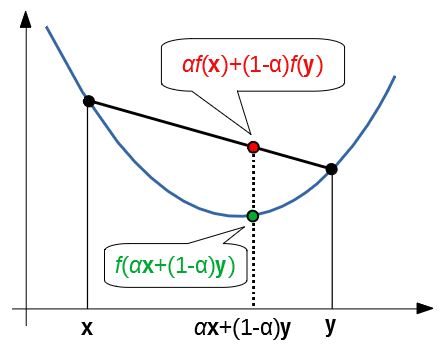
\(\boldsymbol{x}\)と\(\boldsymbol{y}\)を結ぶ線分上の点における位置関係を表している。
証明
それでは「凸計画問題では局所的最適解は大域的最適解である」ことを証明しよう。
(証明)
背理法を用いて示す。
\(\boldsymbol{x}^*\in S\)を凸計画問題\(\{f(\boldsymbol{x})\to\min|\boldsymbol{x}\in S\}\)の局所的最適解とする。
この解とは異なる大域的最適解\(\boldsymbol{y}^*\in S\)が存在して
$$f(\boldsymbol{y}^*)\lt f(\boldsymbol{x}^*)$$
を満たすとする。
このとき、\(f\)は凸関数なので、\(0\le\alpha\le1\)を満たす任意の\(\alpha\)に対して
$$f(\alpha\boldsymbol{x}^*+(1-\alpha)\boldsymbol{y}^*)\le \alpha f(\boldsymbol{x}^*)+(1-\alpha)f(\boldsymbol{y}^*)\lt f(\boldsymbol{x}^*)$$
これは先の仮定と矛盾する。
したがって、局所的最適解は大域的最適解に等しい。
(証明終)
関数の勾配ベクトル
非線形関数の挙動を調べる場合、偏微分を用いる方法が有効である。
\(n\)変数関数\(f(\boldsymbol{x})\)の勾配(ベクトル)を\(\nabla f\)とかき、次式で定義する。
\[
\nabla f=\left(
\begin{array}{c}
\frac{\partial f(\boldsymbol{x})}{\partial x_1} \\
\frac{\partial f(\boldsymbol{x})}{\partial x_2} \\
\vdots \\
\frac{\partial f(\boldsymbol{x})}{\partial x_n}
\end{array}
\right)
\]
勾配ベクトルの方向は、その点での関数\(f\)の増加率が最大となる方向を表す。
\(f\)が1変数関数の場合、勾配は1階微分と同じである。
停留点
\(\nabla f(a)=0\)を満たす\(a\)を、\(f\)の停留点と呼ぶ。
停留点は次のように分類される。
- 極小点：その点の周囲だけを見ると、最小である点
- 極大点：その点の周囲だけを見ると、最大である点
- 鞍点：極小でも極大でもない点
無制約の最適化問題において、局所的最適解は常に停留点である。
ただし、逆は必ずしも成り立たない。
ヘッセ行列
\(n\)変数関数\(f(\boldsymbol{x})\)に対して、次の\(n\)次正方行列をヘッセ行列という。
\[
H(\boldsymbol{x}) = \nabla^2f(\boldsymbol{x}) = \left(
\begin{array}{cccc}
\frac{\partial^2 f(\boldsymbol{x})}{\partial x_1^2} & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_1\partial x_2} & \ldots & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_1\partial x_n} \\
\frac{\partial^2 f(\boldsymbol{x})}{\partial x_2\partial x_1} & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_2^2} & \ldots & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_2\partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f(\boldsymbol{x})}{\partial x_n\partial x_1} & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_n\partial x_2} & \ldots & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_n^2}
\end{array}
\right)
\]
\(f\)が1変数関数の場合、ヘッセ行列は2階微分と同じである。
ヘッセ行列は関数の凸性と深い関係がある。
関数の凸性
関数\(f\)は次のように二次のテイラー展開をすることができる。
$$\tilde{f}(\boldsymbol{x})=f(\bar{\boldsymbol{x}})+\nabla f^T(\boldsymbol{x}-\bar{\boldsymbol{x}})+\frac{1}{2}(\boldsymbol{x}-\bar{\boldsymbol{x}})^T\nabla^2f^T(\boldsymbol{x}-\bar{\boldsymbol{x}})+\cdots$$
すべての点においてヘッセ行列が半正定値、すなわち
$$\boldsymbol{d}^T\nabla^2f(\boldsymbol{x})\boldsymbol{d}\ge0，\boldsymbol{d}\in\mathbb{R}^n$$
が成り立つならば、関数\(f\)は凸関数である。
最適性条件
関数\(f(\boldsymbol{x})\)の最小化を考える。
\(\boldsymbol{x}^*\)が局所的最適解であるための必要条件は
$$\nabla f(\boldsymbol{x})=0$$
となることである。これを一次の最適性条件という。
凸関数の場合は必要十分である。
さらに\(\boldsymbol{x}^*\)が局所的最適解であるための必要条件は、ヘッセ行列が半正定値であることである。
これを二次の最適性条件という。
合わせると、\(\boldsymbol{x}^*\)が局所的最適解であるための条件は
$$\nabla f(\boldsymbol{x}^*)=0 かつ \nabla^2f(\boldsymbol{x}^*)が半正定値$$
となる。
大域的最適解であるための条件は、fが凸関数すなわちヘッセ行列が任意の\(\boldsymbol{x}\)について半正定値となることである。
以上の内容から、制約なし最適化問題を解く流れをまとめる。
１．勾配ベクトル\(\nabla f(\boldsymbol{x})=\boldsymbol{0}\)を満たす解\(\boldsymbol{x}^*\)を求める。
２．ヘッセ行列\(\nabla^2 f(\boldsymbol{x}^*)\)の正値性を調べる。
次回は、制約ありの最適化問題の解法を考えていく。
[mathjax] 前回の記事で非線形計画問題について概説した。 [sitecard subtitle=関連記事 url=https://ramenhuhu.com/math-nlp] 勾配とヘッセ行列を用いて、目的関数が[…]
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー４つのパターン サラスの公式による行列式の計算方法 余因[…]
