重積分①では、重積分の定義について述べました。しかし、重積分の値を定義に基づいて計算することは困難です。
ここから、重積分の実用的な計算方法にを学んでいきたいと思います。
累次積分
重積分を、1変数の積分の繰り返しで計算する方法を累次積分といいます。
定理
$$\phi_1(x)、\phi_2(x)はI=[a,b]上の連続関数で、I上で\phi_1(x)\le\phi_2(x)を満たすとする。$$
$$D=\{(x,y)|x\in I,\phi_1(x)\le y\le\phi_2(x)\}とおく。$$
$$Dの内部で有界かつ連続な関数f(x,y)に対して次のことが成り立つ。$$
$$(1)F(x)=\int_{\phi_1(x)}^{\phi_2(x)}f(x,y)dxdyはI上の連続関数である$$
$$(2)\iint_Df(x,y)dxdy=\int_a^b\left(\int_{\phi_1(x)}^{\phi_2(x)}f(x,y)dy\right)dx$$
定理(2)の右辺を次のようにも書きます。
$$\int_a^b\int_{\phi_1(x)}^{\phi_2(x)}f(x,y)dxdy または \int_a^b dx\int_{\phi_1(x)}^{\phi_2(x)}f(x,y)dy$$
積分の順序変更
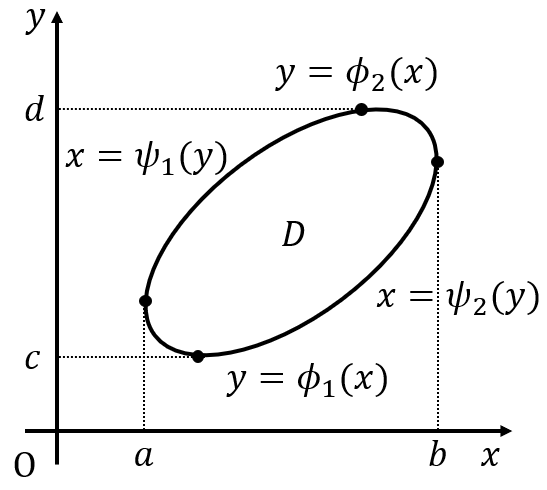
$$Dが[c,d]上の連続関数\psi_1(y)、\psi_2(y)を用いて$$
$$\{(x,y)|c\le y\le d,\psi_1(y)\le x\le\psi_2(y)\}と表されるとき、次式が成り立つ。$$
$$\iint_Df(x,y)dxdy=\int_c^d\left(\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)dx\right)dy$$
したがって、Dがφ(x)とψ(y)のどちらでも表せるとき、次式が成り立つ。
$$\int_a^b\left(\int_{\phi_1(x)}^{\phi_2(x)}f(x,y)dy\right)dx=\int_c^d\left(\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)dx\right)dy$$
このことを、積分の順序変更という。
Dが連続関数f(x)、g(x)により
$$\{(x,y)|a\le x\le b,f(x)\le y\le g(x)\}$$
と表されるとき
$$|D|=\iint_D1dxdy=\int_a^b\left(\int_{f(x)}^{g(x)}1dy\right)dx=\int_a^b\{f(x)-g(x)\}dx$$
計算例
累次積分の計算例をみて理解を深めましょう。
(解)
\[
\begin{align*}
\iint_De^{x+y}dxdy&=\int_0^1\left(\int_0^1e^{x+y}dx \right)dy \\
& =\int_0^1 \left[e^{x+y} \right]_0^1dy=\int_0^1 (e^{1+y}-e^y)dy \\
& =\left[e^{1+y}-e^y \right]_0^1=(e^2-e)-(e-1) \\
& =e^2-2e+1
\end{align*}
\]
(解)
\[
\begin{align*}
\iint_D(x+y)^adxdy &=\int_0^1\left(\int_0^x(x+y)^ady \right)dx \\
& =\int_0^1(a+1)^{-1}\left[ (x+y)^{a+1}\right]_0^xdx \\
& =\int_0^1(a+1)^{-1}\left( (2x)^{a+1}-x^{a+1} \right)dx \\
& =\frac{1}{(a+1)(a+2)}\left[ 2^{a+1}x^{a+2}-x^{a+2}\right]_0^1 \\
& =\frac{1}{(a+1)(a+2)}(2^{a+1}-1)
\end{align*}
\]






