不定積分を学ぶことで、微分方程式を解くことができるようになります。
[mathjax] 今回から、積分法に入っていきます。 まずは不定積分を定義し、積分の計算になれるところから始めたいと思います。 不定積分とは 関数\(f(x)\)に対し、\(F'(x)=f(x)\)を満たす関数\(F(x)[…]
[mathjax] 前回は不定積分の基礎について学びました。 今回は、有理関数・三角関数・無理関数のそれぞれについて積分を行う際の方法について述べていきます。 有理関数 2つの多項式\(P(x)、Q(x)\)の比で表される関[…]
微分方程式とは関数の微分形を含む方程式で、元の関数を求めることを微分方程式を解く、といいます。
微分方程式を解くことで、自然界の様々な法則を導き出していくことができます。まずはその基礎から始め、科学の奥深い世界を楽しむ準備をしていきましょう。
微分方程式の概要
まず用語の定義をしておきます。
常微分方程式
$$xを独立変数とする未知の関数yの導関数y’, y^{\prime\prime}, …を含む方程式$$
$$F(x, y, y’, …, y^{(n)})=0 を常微分方程式という$$
一変数の導関数で記述される方程式を常微分方程式といいます。これに対して、多変数関数の偏微分を含む方程式を偏微分方程式といいます。
$$Fに含まれるy’の導関数の最大階数を、その方程式の階数と呼ぶ$$
たとえば、
$$\frac{d^2 y}{dx^2}-2\frac{dy}{dx}+y=0$$
は2階の常微分方程式です。
微分方程式の解
n階の微分方程式の解で、n個の任意定数を含むものを一般解、任意定数の一部あるいは全てに値を代入して得られる解を特殊解と呼ぶ。
そのいずれでもない解を特異解と呼ぶ。
微分方程式の一般解はある定数を含んだ形で求められます。たとえば
$$y=C_1\cos (\omega t)+C_2\sin (\omega t)$$
のような一般解が得られたとします。ここで、\(t=0\)のとき\(y=0\)、\(t=π/2ω\)のとき\(y=A\)という条件の下では\(C_1、C_2\)を決めることができ
$$y=A\sin (\omega t)$$
となります。これは一つの特殊解で、もちろん元の微分方程式を満たします。
一方、特異解は元の方程式を満たしますが、一般解から求めることができません。\(y=0\)のような自明な解がこれにあたる場合などがあります。
「微分方程式を解く」といった場合は一般解だけでなく特異解も求める必要があり、必ずしも容易に解けるとは限りません。それに、一般解や特異解が容易に見つからないような微分方程式も数多くあります。
まずは、システマティックに解くことのできる簡単な形式のものから慣れていきましょう。
(1) 変数分離形
の形に帰着される微分方程式を、変数分離形と呼びます。
この形では等号の片側に一つの変数をすべて集めることができ、両辺積分して
$$\int \frac{dy}{g(y)}=\int f(x)dx$$
より一般解を得ることができます。
ある点\(y=y_0\)において\(g(y_0)=0\)となるならば、定数関数\(y=y_0\)もまた解となります。
変数分離形の例
(解)
両辺をyで割り、積分します。
$$\int \frac{dy}{y}=\int xdx$$
$$\ln |y|=\frac{1}{2} x^2+C (C:定数)$$
$$|y|=e^{\frac{1}{2} x^2+C}=e^C e^{\frac{1}{2} x^2}$$
\(B=e^C(>0)\)とおき、絶対値を外すと、
$$y=\pm B e^{\frac{1}{2} x^2}$$
\(A=\pm B\)とおくと、\(A\not =0\)で
$$y=Ae^{\frac{1}{2} x^2} (A\not =0)$$
ここで、\(A=0\)のとき\(y=0\)となって元の微分方程式を満たす。
したがって、求める解は
$$y=Ae^{\frac{1}{2} x^2} (A:任意定数)$$
(2) 同次形
の形で表される微分方程式を、同次形と呼びます。
これは\(y/x=u\)とおき、uに関する方程式に変換することで変数分離形に帰着できます。
$$y=xuより、y’=u+xu’$$
よって、解くべき方程式は
$$u’=\frac{f(u)-u}{x}$$
同次形の例
(解)
両辺をxで割ると
$$\frac{dy}{dx}=1+\frac{y}{x}$$
$$u+x\frac{du}{dx}=1+u$$
$$\int du=\int \frac{dx}{x}$$
$$u=\frac{y}{x}=\ln x +C$$
$$y=x(\ln x +C) (C:任意定数)$$
(3) 1階線形微分方程式
1階の導関数を含む線形の微分方程式
$$y’+P(x)y=Q(x)$$
の一般解を求めていきます。
同次方程式と非同次方程式
上式で、\(Q(x)=0\)の場合を同次方程式、\(Q(x)≠0\)の場合を非同次方程式といいます。
同次方程式は変数分離形になっているので、一般解は簡単に求めることができて
$$y=C_1e^{-\int P(x)dx} (C_1:定数)$$
で与えられます。
定数変化法
次に、同次方程式の一般解における定数\(C_1\)をxの関数とみて元の方程式に代入すると、
$$C_1(x)’=Q(x)e^{\int P(x)dx}$$
したがって、一般解として次式を得ます。
$$y=e^{-\int P(x)dx}\left( \int \left( Q(x)e^{\int P(x)dx} \right)dx +C \right)$$
少し複雑だったので、解くときの流れをまとめておきましょう。
- \(Q(x)=0\)とし、同次方程式の一般解を求める
- 同次方程式の一般解の任意定数をxの関数とみて、元の微分方程式に代入する
- 任意定数に関する微分方程式を解き、非同次方程式の一般解を求める
このようにして非同次方程式の一般解を求める方法を、定数変化法と呼びます。
例題:電気回路に関する微分方程式
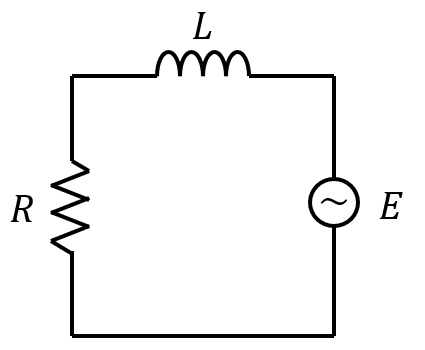
自己インダンクタンスLのコイルと抵抗Rをつないだ直列回路に起電力E(t)を与えるとき、回路に流れる電流I(t)は以下の微分方程式をみたす。
$$\frac{dI(t)}{dt}+\frac{R}{L}I(t)=\frac{1}{L}E(t)$$
1.微分方程式を解き、I(t)を求めよ
2.以下の場合について特殊解を求めよ
(ⅰ)\(E(t)=E_0\)(定数)
(ⅱ)\(E(t)=E_0\sin(\omega t)\)
(解)
1.先ほどの定数変化法を利用して求めます。公式を使い、計算過程は省略します。
$$I(t)=e^{-\frac{R}{L}t} \left( \int \frac{1}{L} E(t)e^{\frac{R}{L}t}dt+C \right)$$
2-(ⅰ)
$$E(t)=E_0のとき、I(t)=\frac{E_0}{R}+Ce^{-\frac{R}{L}t}$$
\(t\to\infty\)のとき、右辺第二項は減衰して0に近づきます。よって、\(I(t)\)はオームの法則による一定値(=電圧/抵抗)になります。
2-(ⅱ)
\(E(t)=E_0\sin(\omega t)\)のとき、
\begin{align*}
I(t)&=\frac{E_0}{R^2+(\omega L)^2}(R\sin (\omega t)-\omega L\cos(\omega t))+Ce^{-\frac{R}{L}t} \\
&=\frac{E_0}{\sqrt{R^2+(\omega L)^2}}\sin (\omega t-\alpha)+Ce^{-\frac{R}{L}t}
\end{align*}
\]
ここで、\(Z=R+i\omega L\) (これを複素インピーダンスという)とおくと、
$$\sqrt{R^2+(\omega L)^2}=|Z|、\alpha=argZ$$
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]





