これまでに学んできた塑性加工の式を用いて、材料の圧縮加工について解析してみよう。
材料の変形領域を平面または球面に沿う薄い板状の要素に分割し、この薄板に作用する応力を主応力と仮定して解析を行う。
このような手法をスラブ法といい、塑性加工の近似解を導くのに用いられる。
ここでは、直方体を平面工具で圧縮する加工を考える。
ブロックの圧縮加工
材料は剛塑性体、工具は剛体とし、\(z\)方向には変形しない平面ひずみ状態を仮定する。
工具-材料間にはクーロン摩擦が働くものとし、摩擦係数を\(\mu\)とする。
直方体材料は高さ\(h\)、幅\(l\)、奥行き\(b\)とする。
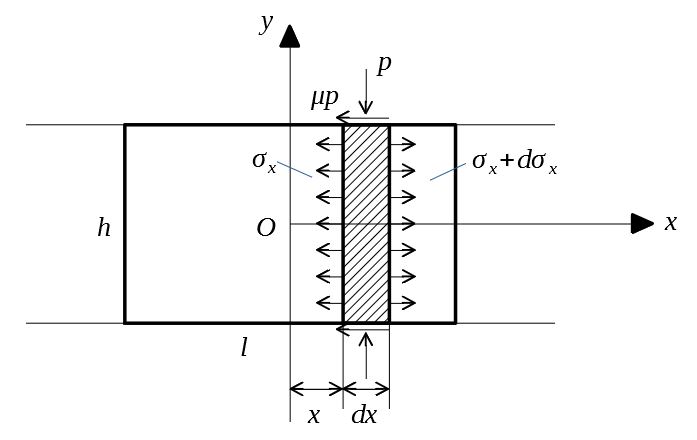
図中の斜線部の板状要素を考える。
この要素の\(x\)方向には、応力\(\sigma_x\)、工具圧力\(p(=-\sigma_y)\)および摩擦応力\(\mu p\)が作用している。\(\sigma_x\)は\(x\)の関数とし、\(\sigma_x\)および\(p\)を主応力とみなす。
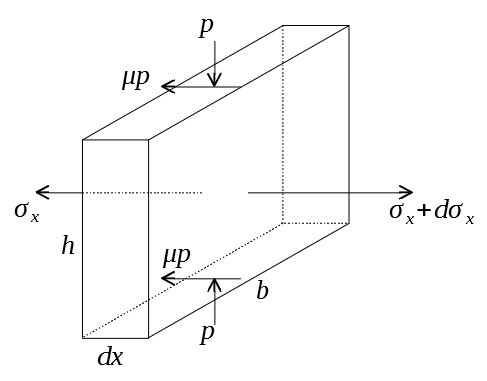
この要素の力のつり合いから、塑性加工に必要な圧縮力を求めてみよう。
\(x\)方向の力のつり合いから
$$(\sigma_x+d\sigma_x)bh-\sigma_xbh-2\mu pbdx=0$$
$$\frac{d\sigma_x}{dx}=\frac{2\mu p}{h} ・・・ ①$$
となる。
降伏条件
この材料がミーゼスの降伏条件に従うとする。
平面ひずみなので
$$d\varepsilon_z=d\gamma_{yz}=d\gamma_{zx}=0$$
である。よってレービー・ミーゼスの式から
$$\sigma_z=\displaystyle\frac{\sigma_x+\sigma_y}{2}=\frac{\sigma_1+\sigma_3}{2}=\sigma_2$$
となり、\(\sigma_z\)は中間主応力である。
ミーゼスの降伏条件式に代入すれば
$$Y^2=\frac{1}{2}\left\{\left(\sigma_1-\frac{\sigma_1+\sigma_3}{2}\right)^2+\left(\frac{\sigma_1+\sigma_3}{2}-\sigma_3\right)^2+\left(\sigma_3-\sigma_1\right)^2\right\}=\frac{3}{4}\left(\sigma_1-\sigma_3\right)^2$$
$$\sigma_1-\sigma_3=\frac{2}{\sqrt{3}}Y=2k$$
となる。
圧力分布
最大主応力は\(\sigma_1=\sigma_x\)、最小主応力は\(\sigma_3=\sigma_y=-p\)であるので、ミーゼスの降伏条件より
$$\sigma_x+p=\frac{2}{\sqrt{3}}Y ・・・② $$
となる。したがって①、②式から
$$\frac{dp}{dx}=-\frac{2\mu}{h}p$$
を得る。
これは変数分離形の微分方程式で
$$p=C_0e^{-\frac{2\mu}{h}x}$$
ここで\(C_0\)は積分定数である。
境界条件は、材料の表面\(x=\frac{l}{2}\)において\(\sigma_x=0,p=\frac{2}{\sqrt{3}}Y\)より
$$\frac{2}{\sqrt{3}}Y=C_0e^{-\frac{\mu l}{h}}$$
$$∴C_0=\frac{2}{\sqrt{3}}Ye^{\frac{\mu l}{h}}$$
したがって、圧力分布の式
$$p=\frac{2}{\sqrt{3}}Y\mathrm{exp}\left\{\frac{2\mu}{h}\left(\frac{l}{2}-x\right)\right\}$$
を得る。
この圧力分布は中央が高い形状を持ち、摩擦が大きいほど高くなる。
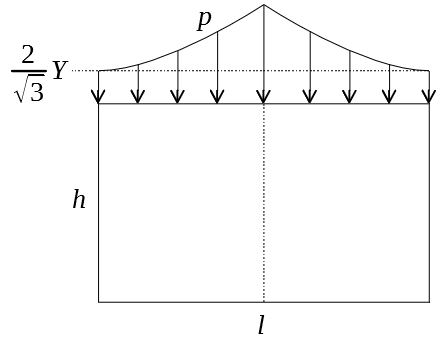
もし摩擦係数がゼロであれば、圧力は\(p=\frac{2}{\sqrt{3}}Y\)のフラットな分布になる。
加工力
材料全体を圧縮変形させるために必要な荷重\(P\)は、上式を積分して得られる。
\begin{align*}
P&=2b\int_{0}^{\frac{l}{2}}pdx \\
&=\frac{4b}{\sqrt{3}}Ye^{\frac{\mu l}{h}}\int_{0}^{\frac{l}{2}}e^{-\frac{2\mu}{h}x}dx \\
&=\frac{4b}{\sqrt{3}}Ye^{\frac{\mu l}{h}}\left(-\frac{h}{2\mu}\right)\left[e^{-\frac{2\mu}{h}x}\right]_{0}^{\frac{l}{2}} \\
&=\frac{2b}{\sqrt{3}}\frac{h}{\mu}Y\left\{\mathrm{exp}\left(\frac{\mu l}{h}\right)-1\right\}
\end{align*}
また、平均圧力\(\bar{p}\)は
$$\bar{p}=\frac{P}{bl}=\frac{2}{\sqrt{3}}\frac{h}{\mu l}Y\left\{\mathrm{exp}\left(\frac{\mu l}{h}\right)-1\right\}$$
となる。
これより、材料が薄くなるほど、また摩擦が大きくなるほど圧力が増大して大きな加工力が必要になることがわかる。
固着領域が存在する場合
工具と材料の間に生じる摩擦応力が、材料のせん断降伏応力\(k\)よりも大きくなる場合、工具に接した表層部分で降伏してすべる現象が発生する。これを固着という。
固着が発生する場合の解を求めてみよう。
\(0\le x\le x_f\)が固着領域、\(x_f\le x\le \frac{l}{2}\)がすべり領域になっているとする。
境界\(x=x_f\)までの範囲では、摩擦応力がせん断降伏応力に等しいので
$$\mu (p)_{x=x_f}=k=\frac{Y}{\sqrt{3}}$$
となる。よって、先に求めた圧力分布の式から
\begin{align*}
\mu\frac{2}{\sqrt{3}}Y\mathrm{exp}\left\{\frac{2\mu}{h}\left(\frac{l}{2}-x_f\right)\right\}&=\frac{Y}{\sqrt{3}} \\
\mathrm{exp}\left\{\frac{2\mu}{h}\left(\frac{l}{2}-x_f\right)\right\}&=\frac{1}{2\mu} \\
\frac{2\mu}{h}\left(\frac{l}{2}-x_f\right)&=-\ln 2\mu \\
∴x_f=\frac{l}{2}+\frac{h}{2\mu}\ln 2\mu
\end{align*}
固着領域\(x_f\)が得られる。
圧力分布
固着領域での圧力分布を求めよう。
力のつり合いより
$$(\sigma_x+d\sigma_x)bh-\sigma_xbh-\frac{2}{\sqrt{3}}Ybdx=0$$
$$\frac{d\sigma_x}{dx}=\frac{2}{\sqrt{3}}Y\frac{1}{h}$$
を得る。先ほどと同様にミーゼスの降伏条件を適用して積分すると
$$\frac{dp}{dx}=-\frac{2}{\sqrt{3}}Y\frac{1}{h}$$
$$p=-\frac{2}{\sqrt{3}}Y\frac{1}{h}x+C_1$$
となる。
積分定数\(C_1\)は\(x=x_f\)で\(p\)が連続となることから定めることができる。すなわち
\begin{align*}
-\frac{2}{\sqrt{3}}Y\frac{1}{h}x_f+C_1&=\frac{2}{\sqrt{3}}Y\mathrm{exp}\left\{\frac{2\mu}{h}\left(\frac{l}{2}-x_f\right)\right\} \\
&=\frac{2}{\sqrt{3}}Y\mathrm{exp}\left\{-\ln 2\mu\right\} \\
&=\frac{2}{\sqrt{3}}Y\frac{1}{2\mu} \\
∴C_1&=\frac{2}{\sqrt{3}}Y\frac{1}{h}\left(\frac{h}{2\mu}+x_f\right)
\end{align*}
したがって
$$p=\frac{2}{\sqrt{3}}Y\frac{1}{h}\left(\frac{h}{2\mu}+x_f-x\right)$$
となる。
一方、すべり領域では先の式がそのまま利用可能である。
加工力
固着が生じる場合に必要な荷重は
\begin{align*}
P&=2b\left[\frac{2}{\sqrt{3}}Y\frac{1}{h}\int_{0}^{x_f}\left(\frac{h}{2\mu}+x_f-x\right)dx+\frac{2}{\sqrt{3}}Y\int_{x_f}^{\frac{l}{2}}\mathrm{exp}\left\{\frac{2\mu}{h}\left(\frac{l}{2}-x\right)\right\}dx\right] \\
&=\frac{2}{\sqrt{3}}Y\frac{bh}{\mu}\left\{\left(\frac{1}{2\mu}-1\right)+\frac{x_f}{h}+\mu\left(\frac{x_f}{h}\right)^2\right\}
\end{align*}
となる。また、平均圧力は
$$\bar{p}=\frac{P}{bl}=\frac{2}{\sqrt{3}}Y\frac{h}{\mu l}\left\{\left(\frac{1}{2\mu}-1\right)+\frac{x_f}{h}+\mu\left(\frac{x_f}{h}\right)^2\right\}$$
となる。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]




