金属材料に力を加えていくと、初めに弾性変形した後、ある応力で塑性変形が開始する。
これを降伏(yielding)といい、このときの応力を降伏応力(yield stress)と呼んだ。一軸試験で得られる応力ひずみ線図を用いた解説は別記事を参照。
[mathjax] 材料の機械的特性を知るために一軸引張試験がよく用いられる。 丸棒やダンベル型に加工した材料に対し、引張試験機を用いて荷重をかけて変形量を測定することで、応力とひずみの関係を得る試験である。 応力を縦軸、[…]
この記事では、材料が降伏しているかどうかを判定する方法について学んでいこう。
式自体はそれほど難しいわけではないが、考え方を理解するのにやや苦労するかもしれないので可能な限り丁寧に説明したい。
降伏条件とは
材料が降伏する応力を決定する式を降伏条件(yield criterion)という。
未変形材の降伏応力を\(Y\)とすると、例えばx方向の一軸引張における降伏条件は
$$\sigma_x=Y$$
と表すことができる。塑性変形をしている物体は、常に降伏条件を満たす応力状態をとり、任意の応力状態となることはない。
ところで、実際の変形は単純な一軸応力ではなく多軸応力状態下で生じるため、降伏条件は多軸応力に対する関数として定義される。
$$f(\sigma_{ij})=Y$$
これを降伏関数といい\(f\lt Y\)であれば弾性、\(f=Y\)であれば降伏していることを意味する。この関数が応力空間に描く曲面を降伏曲面という。
よく用いられる代表的なものに、トレスカの降伏条件とミーゼスの降伏条件がある。
以下では、これらの降伏条件の定義や解釈、使い方について解説する。
トレスカの降伏条件
材料の最大せん断応力が一定値に達すると降伏するという条件を、トレスカ(Tresca)の降伏条件または最大せん断応力説という。
一軸引張における降伏応力を\(Y\)として
と表される。ただし\(\sigma_{max},\sigma_{min}\)は最大・最小主応力、\(k\)はせん断降伏応力である。
主応力は応力テンソルの3つの固有値であり、これに対応する固有ベクトルが主応力軸となる。主応力状態ではせん断成分がすべて0となる。詳細は後述する。
ミーゼスの降伏条件
材料のせん断ひずみエネルギーが一定値に達すると降伏するという条件を、ミーゼス(Mises)の降伏条件またはせん断ひずみエネルギー説という。
主応力状態におけるミーゼスの降伏条件は次式で表される。
$$Y=\bar{\sigma}=\sqrt{\frac{1}{2}\left\{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2\right\}}$$
ここで\(\bar{\sigma}\)は相当応力(equivalent stress)や有効応力、ミーゼス応力などと呼ばれる量である。
相当応力は、多軸応力状態から一軸応力に「相当」する値を得る変換式として解釈することもできる。静水圧状態では\(\bar{\sigma}=0\)、一軸引張\((\sigma_1=\sigma,\sigma_2=\sigma_3=0)\)では\(\bar{\sigma}=\sigma\)となる。
ミーゼスの降伏条件は、『相当応力\(\bar{\sigma}\)が降伏応力\(Y\)に達すると材料は降伏して塑性変形する。\(Y\)以下では塑性変形しない』ことを意味する。
なお、一般の座標系に対しては次式となる。
$$Y=\bar{\sigma}=\sqrt{\frac{1}{2}\left\{(\sigma_x-\sigma_y)^2+(\sigma_y-\sigma_z)^2+(\sigma_z-\sigma_x)^2+6(\tau_{xy}^2+\tau_{yz}^2+\tau_{zx}^2)\right\}}$$
また、偏差応力テンソルの2次不変量\(J_2\)を用いて
$$\bar{\sigma}=\sqrt{3}\left|J_2\right|^{1/2}$$
とも表される。
計算問題
ミーゼスの式を使った簡単な計算を解いてみよう。
ある材料が平面応力状態で塑性変形をしている。
$$\sigma_x=200~\mathrm{MPa},\sigma_y=-350~\mathrm{MPa},\tau_{xy}=50~\mathrm{MPa}$$
のとき、変形抵抗を求めよ。
平面応力状態なので、\(\sigma_z=\tau_{yz}=\tau_{zx}=0\)である。
(解)
ミーゼスの降伏条件式から
\begin{align*}
Y^2=\bar{\sigma}^2&=\frac{1}{2}\left\{(\sigma_x-\sigma_y)^2+(\sigma_y-\sigma_z)^2+(\sigma_z-\sigma_x)^2+6(\tau_{xy}^2+\tau_{yz}^2+\tau_{zx}^2)\right\} \\
&=\frac{1}{2}(550^2+200^2+350^2+6・50^2)=240000 \\
∴\bar{\sigma}&=489.9~\mathrm{MPa}
\end{align*}
(終)
降伏曲面
降伏条件が応力空間で描く曲面が降伏曲面である。
ミーゼスの降伏条件は円柱、トレスカの降伏条件は六角柱をなす。曲面の内側では弾性変形を、曲面上で降伏する。
簡単のために、平面応力状態\((\sigma_3=0)\)における曲線を考えてみよう。
ミーゼスの降伏条件式は
$$\frac{1}{2}\left\{(\sigma_1-\sigma_2)^2+(\sigma_2-0)^2+(0-\sigma_1)^2\right\}=Y^2$$
$$\sigma_1^2-\sigma_1\sigma_2+\sigma_2^2-Y^2=0$$
これは、原点のまわりに楕円を\(\pi/4\)だけ回転した楕円を表す。二次曲線の取り扱いについては以下の記事を参照。
[mathjax] 2次形式の標準化を利用すると、二次曲線を明快に取り扱うことができるようになる。 この記事では、二次曲線の分類や標準形への変形、図形的意味などについて学んでいく。 2次形式の標準化について復習したい方は以[…]
図示すると下のようになる。
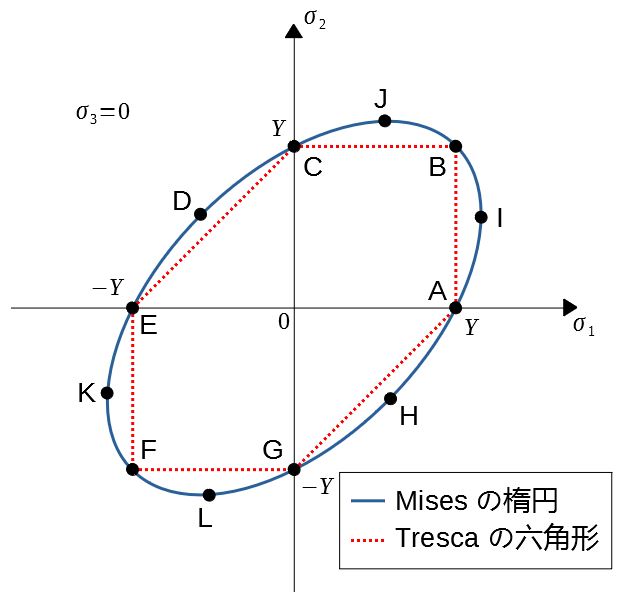
図中の各点における状態は
\begin{cases}
A,C,E,G&:一軸引張・圧縮 \\
I,J,K,L&:平面ひずみ \\
B,F&:等二軸引張・圧縮 \\
D,H&:引張圧縮
\end{cases}
である。
例えば\(\sigma_1\)方向の一軸引張では、原点から出発して点\(A\)に向かっている最中は弾性変形、点\(A\)に達すると塑性変形が開始する、というように考える。
このときに描く応力の軌跡を応力経路という。
加工硬化則
未変形材が初めて降伏するときの条件を初期降伏条件という。
金属材料では塑性加工に伴って変形抵抗が増加する、加工硬化(またはひずみ硬化)という現象が発生する。
そこで、塑性変形開始後の降伏曲面を与える、後続降伏条件を考える必要がある。様々な加工硬化則により後続降伏曲面を表現する。
等方硬化則
後続降伏曲面が等方的に拡大するものを等方硬化則という。数式の取り扱いが容易で利用しやすいが、バウシンガー効果を表現できないなどといったデメリットがある。
移動硬化則
降伏曲面の形状や大きさが変化せず、中心が移動するものを移動硬化則という。バウシンガー効果を表現することができる。
異方硬化則
実際の材料では、後続降伏曲面の形状は複雑な変化がみられる。負荷経路やひずみ量によっても異なり、これを数式で表現することは容易ではない。
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]





