前回はブロック材の加工解析を行った。
[mathjax] これまでに学んできた塑性加工の式を用いて、材料の圧縮加工について解析してみよう。 材料の変形領域を平面または球面に沿う薄い板状の要素に分割し、この薄板に作用する応力を主応力と仮定して解析を[…]
今回は、丸棒や円管といった軸対称な塑性変形を考える。軸対称加工における主応力の方向は、半径方向・接線方向・軸方向になる。
ここでは、円柱の圧縮加工の解析を行う。
円柱の圧縮加工
円柱形状の材料を平行工具で圧縮する場合を考える。材料は剛塑性体、工具は剛体とする。
工具-材料間にはクーロン摩擦が働くものとし、摩擦係数を\(\mu\)とする。
材料は高さ\(h\)、半径\(r_0\)とする。
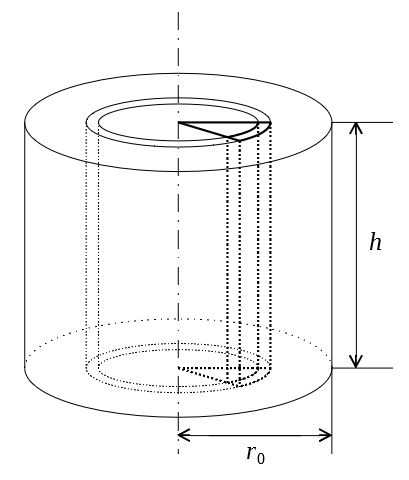
図の微小な円筒状要素について考える。
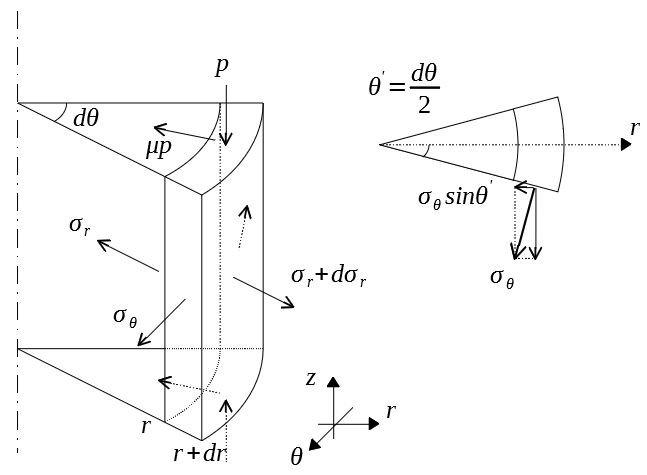
\(r\)方向の力のつり合いは
$$(\sigma_r+d\sigma_r)(r+dr)d\theta・h-\sigma_r・rd\theta・h-2\mu prd\theta・h-2\sigma_{\theta}\sin\frac{d\theta}{2}・dr・h=0$$
ここで
$$(\sigma_r+d\sigma_r)(r+dr)d\theta・h≒\sigma_r・rd\theta・h+rd\sigma_rd\theta・h$$
および\(d\theta\)が微小なので
$$\sin\frac{d\theta}{2}≒\frac{d\theta}{2}$$
を用いて整理すると、次式を得る。
$$\frac{d\sigma_r}{dr}+\frac{\sigma_r-\sigma_{\theta}}{r}-\frac{2\mu p}{h}=0 ・・・ ①$$
この式を解くために、軸対称変形における降伏条件を考える。
降伏条件
半径\(r\)の位置での微小変位を\(u_r\)とすると
$$d\varepsilon_r=\frac{du_r}{dr},d\varepsilon_{\theta}=\frac{u_r}{r}$$
である。よって、体積一定条件より
$$\frac{du_r}{dr}+\frac{u_r}{r}+d\varepsilon_z=0$$
\(d\varepsilon_z\)を\(r\)に依存しない定数と仮定して、この線形微分方程式を解くと
$$u_r=-\frac{d\varepsilon_z}{2}r+\frac{C_0}{r}$$
となる。積分定数\(C_0\)は、\(r=0\)で\(u_r=0\)より\(C_0=0\)である。これより
$$d\varepsilon_r=\frac{du_r}{dr}=-\frac{d\varepsilon_z}{2},d\varepsilon_{\theta}=\frac{u_r}{r}=-\frac{d\varepsilon_z}{2}$$
と\(d\varepsilon_r=d\varepsilon_{\theta}\)であることがわかる。レービー・ミーゼスの式から
$$\frac{d\varepsilon_r}{\sigma_r-\sigma_m}=\frac{d\varepsilon_{\theta}}{\sigma_{\theta}-\sigma_m}$$
$$∴\sigma_r=\sigma_{\theta} ・・・ ②$$
となる。
これをミーゼスの降伏条件式に代入すると
$$Y^2=\frac{1}{2}\left\{(\sigma_r-\sigma_{\theta})^2+(\sigma_{\theta}-\sigma_z)^2+(\sigma_z-\sigma_r)^2\right\}=(\sigma_r-\sigma_z)^2$$
$$Y=|\sigma_r-\sigma_z|$$
を得る。なお、トレスカの降伏条件でも同じ式になる。
いまは圧縮加工を考えているので、\(\sigma_z=-p\lt\sigma_r\)から
$$Y=\sigma_r+p$$
加工硬化を無視すれば\(Y\)は\(r\)によらない。両辺を\(r\)で微分して
$$\frac{d\sigma_r}{dr}=-\frac{dp}{dr} ・・・ ③$$
となる。
圧力分布
①、②、③式から
$$\frac{dp}{dr}+\frac{2\mu p}{h}=0$$
積分して
$$p=C_1\mathrm{exp}\left(-\frac{2\mu}{h}r\right)$$
\(r=r_0\)で\(\sigma_r=0\)すなわち\(p=Y\)であることから、積分定数\(C_1\)が求まる。
以上より、圧力分布の式が導かれる。
加工力
材料全体を圧縮変形させるために必要な圧下力\(P\)は、上式を積分して得られる。
\begin{align*}
P&=\int_0^{r_0}2\pi rpdr \\
&=2\pi Y\int_0^{r_0}r\mathrm{exp}\left\{\frac{2\mu(r_0-r)}{h}\right\}dr \\
&=2\pi Y\left[\left.-\frac{h}{2\mu}r\mathrm{exp}\left\{\frac{2\mu(r_0-r)}{h}\right\}\right|_{r=0}^{r=r_0}+\frac{h}{2\mu}\int_0^{r_0}\mathrm{exp}\left\{\frac{2\mu(r_0-r)}{h}\right\}dr\right] \\
&=2\pi Y\left[\left.-\frac{h}{2\mu}r_0-\frac{h^2}{4\mu^2}\mathrm{exp}\left\{\frac{2\mu(r_0-r)}{h}\right\}\right|_{r=0}^{r=r_0}\right] \\
&=\frac{\pi h^2Y}{2\mu^2}\left\{\mathrm{exp}\left(\frac{2\mu r_0}{h}\right)-\frac{2\mu r_0}{h}-1\right\}
\end{align*}
となる。
また、平均圧力\(\bar{p}\)は
$$\bar{p}=\frac{P}{\pi r_0^2}=\frac{Y}{2}\left(\frac{h}{\mu r_0}\right)^2\left\{\mathrm{exp}\left(\frac{2\mu r_0}{h}\right)-\frac{2\mu r_0}{h}-1\right\}$$
となる。
固着領域が存在する場合
端面での摩擦が大きく、固着が生じる場合について考える。
固着領域とすべり領域の境界を\(r=r_f\)とすると、点\(r_f\)における摩擦せん断応力が材料のせん断降伏応力\(k=Y/\sqrt{3}\)に等しいので
$$\mu (p)_{r=r_f}=\frac{Y}{\sqrt{3}}$$
よって、先に求めた圧力分布の式に代入して
\begin{align*}
\mu Y\mathrm{exp}\left\{\frac{2\mu(r_0-r_f)}{h}\right\}&=\frac{Y}{\sqrt{3}} \\
\mathrm{exp}\left\{\frac{2\mu(r_0-r_f)}{h}\right\}&=\frac{1}{\sqrt{3}\mu} \\
\frac{2\mu(r_0-r_f)}{h}&=-\ln\sqrt{3}\mu \\
∴r_f=r_0+\frac{h}{2\mu}\ln\sqrt{3}\mu
\end{align*}
を得る。
圧力分布
固着領域\((0\le r\le r_f)\)での圧力分布は
$$\frac{dp}{dr}+\frac{2\mu p}{h}=\frac{dp}{dr}+\frac{2Y}{\sqrt{3}h}=0$$
を積分して
$$p=-\frac{2Y}{\sqrt{3}h}r+C_2$$
すべり領域での圧力分布は先に求めた式がそのまま成り立つ。
\(r=r_f\)で連続となることから、積分定数\(C_2\)は
$$-\frac{2Y}{\sqrt{3}h}r_f+C_2=Y\mathrm{exp}\left\{\frac{2\mu(r_0-r_f)}{h}\right\}$$
\begin{align*}
C_2&=Y\mathrm{exp}\left\{\frac{2\mu(r_0-r_f)}{h}\right\}+\frac{2Y}{\sqrt{3}h}r_f \\
&=Y\mathrm{exp}\left\{\frac{2\mu(r_0-r_0-\frac{h}{2\mu}\ln\sqrt{3}\mu)}{h}\right\}+\frac{2Y}{\sqrt{3}h}r_f \\
&=\frac{Y}{\sqrt{3}\mu}+\frac{2Y}{\sqrt{3}h}r_f
\end{align*}
と定められる。したがって
$$p=\frac{2Y}{\sqrt{3}h}\left(\frac{h}{2\mu}+r_f-r\right) (0\le r\le r_f)$$
となる。
加工力
材料全体を圧縮変形するために必要な圧下力は積分して求められる。
$$P=Y\pi r_f^2\left(\frac{2\sqrt{3}}{9}\frac{r_f}{h}+\frac{1}{\sqrt{3}\mu}\right)+\frac{Y}{2}\frac{\pi h^2}{\mu^2}\left\{\frac{1}{\sqrt{3}\mu}\left(\frac{2\mu}{h}r_f+1\right)-\frac{2\mu}{h}r_0-1\right\}$$
平均圧力は\(\pi r_0^2\)で割ればよい。
- (積分計算の詳細)
-
\begin{align*}
P&=\int_0^{r_f}2\pi r・\frac{2Y}{\sqrt{3}h}\left(\frac{h}{2\mu}+r_f-r\right)dr+\int_{r_f}^{r_0}2\pi r・Y\mathrm{exp}\left\{\frac{2\mu(r_0-r)}{h}\right\}dr \\
&=\frac{4\pi Y}{\sqrt{3}h}\int_0^{r_f}\left\{\left(\frac{h}{2\mu}+r_f\right)r-r^2\right\}dr+2\pi Y\left[\left[-\frac{h}{2\mu}r\mathrm{exp}\left\{\frac{2\mu(r_0-r)}{h}\right\}\right]_{r_f}^{r_0}+\frac{h}{2\mu}\int_{r_f}^{r_0}\mathrm{exp}\left\{\frac{2\mu(r_0-r)}{h}\right\}dr\right] \\
&=\frac{4\pi Y}{\sqrt{3}h}\left[\left(\frac{h}{4\mu}+\frac{1}{2}r_f\right)r^2-\frac{1}{3}r^3\right]_0^{r_f}+2\pi Y\left[-\frac{h}{2\mu}r_0+\frac{h}{2\mu}r_f\mathrm{exp}\left\{\frac{2\mu(r_0-r_f)}{h}\right\}-\frac{h^2}{4\mu^2}\left[\mathrm{exp}\left\{\frac{2\mu(r_0-r)}{h}\right\}\right]_{r_f}^{r_0}\right] \\
&=\frac{4\pi Y}{\sqrt{3}h}\left(\frac{h}{4\mu}r_f^2+\frac{1}{2}r_f^3-\frac{1}{3}r_f^3\right)+2\pi Y\left[-\frac{h}{2\mu}r_0+\frac{h}{2\mu}r_f・\frac{1}{\sqrt{3}\mu}-\frac{h^2}{4\mu^2}\left(1-\frac{1}{\sqrt{3}\mu}\right)\right] \\
&=Y\pi r_f^2\left(\frac{2\sqrt{3}}{9}\frac{r_f}{h}+\frac{1}{\sqrt{3}\mu}\right)+\frac{Y}{2}\frac{\pi h^2}{\mu^2}\left\{\frac{1}{\sqrt{3}\mu}\left(\frac{2\mu}{h}r_f+1\right)-\frac{2\mu}{h}r_0-1\right\}
\end{align*}
金属の変形に関する内容です。 塑性加工学 弾性変形と塑性変形の違い-ミクロとマクロな視点から 応力・ひずみの定義と意味、求め方を解説 公称応力‐真応力、公称ひずみ‐真ひずみの変換方法と注意点 応力ひずみ線図を読み解くポ[…]




