ひずみ速度と渦度の定義
(1)垂直ひずみ
垂直ひずみ
は、伸びや圧縮といった体積の変化を表す。
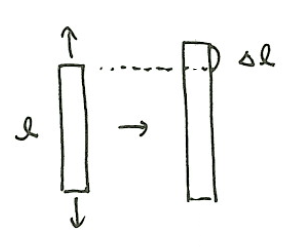
長さ\(l\)の要素が\(\Delta l\)だけ伸びたときのひずみを
$$\varepsilon=\frac{\Delta l}{l}$$
で与える。
x方向について、
$$\varepsilon_x=\frac{\Delta l_x}{l_x}=\frac{\frac{\partial u}{\partial x}dxdt}{dx}=\frac{\partial u}{\partial x}dt$$
よって、ひずみ速度は次式で与えられる。
$$\dot{\varepsilon_x}=\frac{\varepsilon_x}{dt}=\frac{\partial u}{\partial x}$$
$$\dot{\varepsilon_y}=\frac{\varepsilon_y}{dt}=\frac{\partial v}{\partial y}$$
(2)せん断ひずみ
せん断ひずみ
は変形の角度変化を表し、体積の変化には寄与しない。
せん断ひずみ速度は、次式で与えられる。
$$\dot{\gamma}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}$$
(3)渦度
渦度
は回転を表す。ベクトル解析のrotを用いて以下で定義する。
\(\mathbf{U}=(u, v)\)として
$$\zeta=rot\mathbf{U}=\nabla×\mathbf{U}=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}$$
渦度ζは、回転の角速度ωの2倍に等しい。
$$\omega=\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)=\frac{1}{2}\zeta$$
ζ=0のとき、無渦運動となる。これをポテンシャル流という。
ζ≠0のときは渦運動となる。
循環
循環Γ
は、次式で定義される。ベクトルの線積分を参照。
$$\Gamma=\oint\mathbf{U}・d\mathbf{s}=\oint U\cos\theta ds$$
\(\mathbf{U}=(u, v)\)、\(d\mathbf{s}=(dx, dy)\)より、次のように書ける。
$$\Gamma=\oint\mathbf{U}・d\mathbf{s}=\oint(udx+vdy)$$
循環Γとは、流れの方向であるs軸上の合速度Uによる線積分そのものである。
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]




