垂直衝撃波については以下の記事を参照ください。
[mathjax] 衝撃波 圧力などが不連続に急変する現象を衝撃といい、その断面を衝撃波と呼ぶ。 衝撃波は、波面と伝播方向によって垂直衝撃波・斜め衝撃波・離脱衝撃波に分類できる。 [sitecard subtitle=関連記[…]
この記事では、発展形として斜め方向の衝撃波を定式化する。
斜め衝撃波
くさびや円錐のように傾きを持つ物体に沿って流体が流れるとき、壁面に沿って圧縮を受けることで斜めの衝撃波が発生する。
先に垂直衝撃波でみたように、衝撃波面の前後で物理量がどのように変化するかを定式化していく。
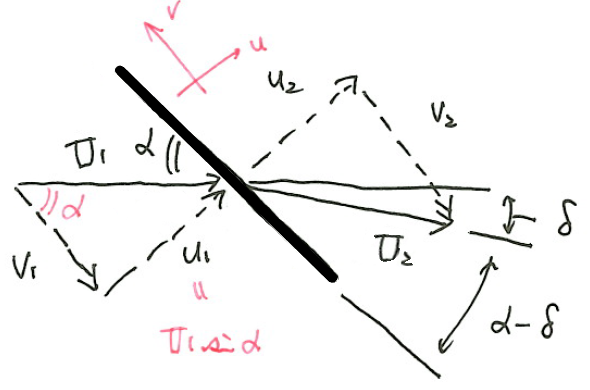
図のように、速度\(U_1\)の流れが衝撃波面を境に角度\(\delta\)だけ向きを変えて速度\(U_2\)の流れに変化したとする。
元の流れの向きと衝撃波面のなす角を\(\alpha\)とする。衝撃波面と垂直な向きを\(u\)方向、平行な向きを\(v\)方向とし、\(U_1\)および\(U_2\)を\(u、v\)方向成分に分解する。
\(\delta、\alpha\)をそれぞれ流れの転向角、衝撃波角とよぶ。
このとき、\(v\)方向は衝撃波面の影響を受けないため、
$$v_1=v_2=v=const$$
とすることができる。これより、考えるべきは\(u\)方向のみであり、垂直な衝撃波と同じ考え方を適用できることがわかる。
さて、速度成分\(u_1\)の点での音速を\(c_1\)とし、その比であるマッハ数を考えると
$$\frac{u_1}{c_1}=\frac{U_1\sin\alpha}{c_1}=M_1\sin\alpha$$
となる。よって、垂直衝撃波で導いた式において、MをMsinαで置き換えることで斜め衝撃波の式を導くことができる。
斜め衝撃波が発生する条件
斜め衝撃波が発生するのは、
$$\frac{u_1}{c_1}\ge 1 ⇔ U_1\sin\alpha\ge c_1$$
のときである。
これより、衝撃波角\(\alpha\)のとる範囲がわかる。
$$\frac{u_1}{c_1}=\frac{U_1}{c_1}\sin\alpha=M_1\sin\alpha\ge 1$$
$$∴\alpha\ge\sin^{-1}\left(\frac{1}{M_1}\right)$$
したがって
である。ただし\(\alpha=\pi/2\)は垂直衝撃波を表す。
流れの転向角と衝撃波角の関係
転向角\(\delta\)と衝撃波角\(\alpha\)の間の関係式を導く。
$$u_2=U_2\sin (\alpha-\delta)$$
より、
$$\frac{u_2}{c_2}=\frac{U_2}{c_2}\sin (\alpha-\delta)=M_2\sin (\alpha-\delta)$$
\(M_1\to M_1\sin\alpha、M_2\to M_2\sin(\alpha-\delta)\)とすることで、M1とM2の関係式は
ここで、
$$\tan\alpha=\frac{u_1}{v_1}=\frac{u_1}{v} ,\tan(\alpha-\delta)=\frac{u_2}{v_2}=\frac{u_2}{v}$$
および圧力比の式を用いて
$$\frac{\tan(\alpha-\delta)}{\tan\alpha}=\frac{u_2}{u_1}$$
から
ただし、\(\alpha=\pi/2\)で\(\delta=0\)(垂直衝撃波)である。
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]




