ジューコフスキー(Joukowski)変換
翼の周りの流体運動を考えるときに、流れの写像という概念を用いることで、複雑な物体周りの流れを解析することができる。
ジューコフスキー変換は
$$\zeta=z+\frac{a^2}{z}$$
という形で表され、\(z(x, y)\)平面と\(\zeta(\xi, \eta)\)平面の二つの複素数平面の写像を表す。
この変換式を用いると、円柱から平板や翼などへ変換することができ、平板翼やジューコフスキー翼まわりの流れを知ることができる。
(1)平板への写像
\(z\)平面上で、原点中心、半径\(a\)の円を写像する。
$$z=ae^{i\theta}$$
とおくと、
\[
\begin{align*}
\zeta & =z+\frac{a^2}{z} \\
& =ae^{i\theta}+ae^{-i\theta} \\
& =a(\cos\theta+i\sin\theta)+a(\cos\theta-i\sin\theta) \\
& =2a\cos\theta
\end{align*}
\]
したがって
$$\xi=2a\cos\theta ,\eta=0$$
となる。すなわち、厚みのない長さ4aの平板に写像される。
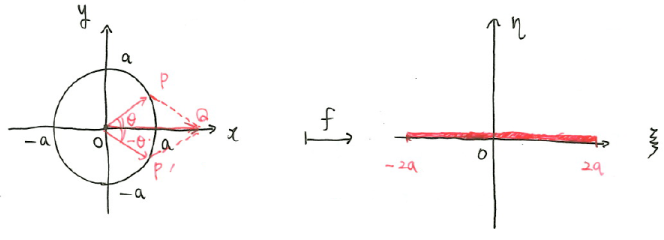
(2)円弧への写像
\(z\)平面上で、\(y\)軸上に中心をもつ半径\(a_0\)の円を写像する。
$$z:x^2+(y-m)^2=a_0^2$$
\(y=m\)に中心があり、\(x=\pm a\)を通るとする。
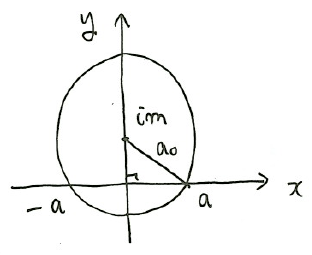
まず、\(x=\pm a\)は\(\xi=\pm 2a\)に写像される。\(z\)平面の原点に対する円周上の位置\(z\)は、
$$z=im+a_oe^{i\theta}$$
と書ける。また、図より
$$a^2=a_0^2-m^2$$
である。これらを用いると
$$\zeta=(im+a_oe^{i\theta})+\frac{a_0^2-m^2}{im+a_oe^{i\theta}}$$
\(\theta=\pi/2\)において、\(\zeta=2mi\)より、\(z(0, m)\)は\(\zeta(0, 2m)\)へ写像される。この\(2m\)を円弧のそりの量と呼ぶ。
ここで、
$$\frac{\zeta-2a}{\zeta+2a}=\frac{z+\frac{a^2}{z}-2a}{z+\frac{a^2}{z}+2a}=\left(\frac{z-a}{z+a}\right)^2 …(*)$$
である。図のように、\(z=\pm a\)に対応する円周上の位置を
$$z=-a+\rho_1e^{i\theta_1} ,z=a+\rho_2e^{i\theta_2}$$
とし、\(\zeta=\pm 2a\)に対応する位置を
$$\zeta=-2a+r_1e^{i\alpha_1} ,\zeta=2a+r_2e^{i\alpha_2}$$
とする。
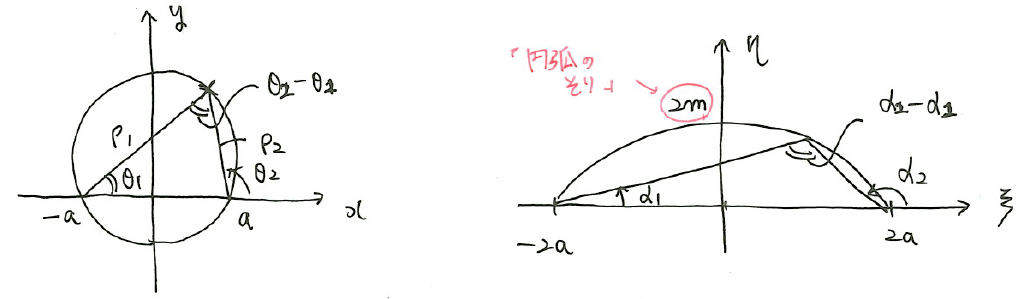
(*)式に代入すると、
$$\left(\frac{\rho_2}{\rho_1}\right)^2e^{i2(\theta_2-\theta_1)}=\frac{r_2}{r_1}e^{i(\alpha_2-\alpha_1)}$$
$$\theta_2-\theta_1=\frac{1}{2}(\alpha_2-\alpha_1)$$
円周角は一定なので、\(\theta_2-\theta_1=const\)、よって\(\alpha_2-\alpha_1=const\)である。すなわち、\(\zeta\)平面では円弧に写像される。
(3)ジューコフスキー翼
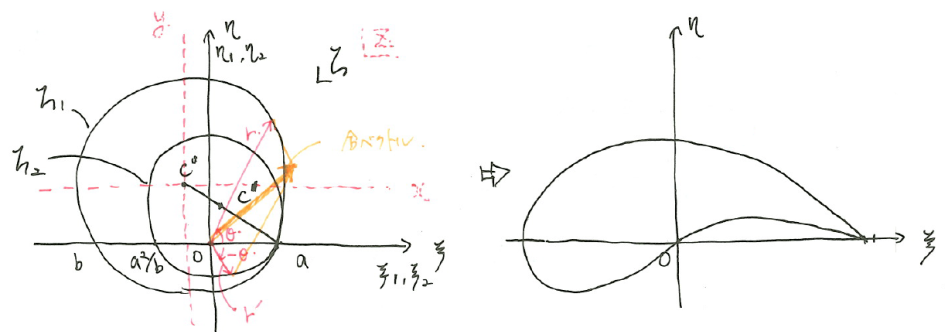
\(z\)平面上で、\(x,y\)軸上に中心がない半径\(a_0\)の円を写像する。ただし、\(x\)軸と\(x=a(>0)、x=b(<a)\)で交点を持つとする。
$$\zeta=z+\frac{a^2}{z}$$
において、
$$\zeta_1=z ,\zeta_2=\frac{a^2}{z}$$
とする。
\(z=re^{i\theta}\)とし、\(rr’=a^2\)となる\(r’\)を用いて写像を行うと
$$\zeta=\zeta_1+\zeta_2=re^{i\theta}+r’e^{-i\theta}$$
ここで、\(\zeta_1\)は、\(\xi\)軸となす角度が\(\theta\)である長さ\(r\)の動径を表し、\(\zeta_2\)は、\(\xi\)軸となす角度が\(-\theta\)である長さ\(r’\)の動径を表す。
ただし、\(r’=a/r\)は点\((a, 0)、(a^2/b, 0)\)を通り、\(z\)平面の円の中心と\((a, 0)\)を結ぶ直線上に中心をもつ円の軌跡を描く。
翼に作用する揚力と抗力
速度\(U\)の一様流の中に翼があるとする。このとき、翼には揚力および抗力が働く。
翼の部位の名称
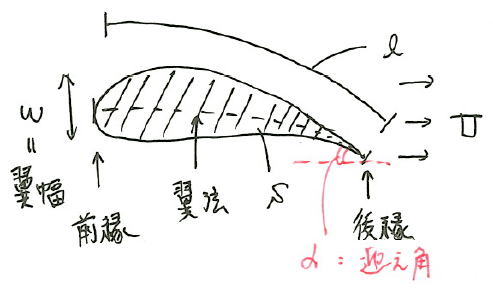
まず、翼の部位の名称を上図のように定義する。翼の両端を前縁、後縁といい、前縁と後縁を結ぶ直線を翼弦という。翼の幅を翼幅(w)、全長を翼弦長(l)といい、翼面積をSとする。一様流に対する翼の角度αを迎え角という。
揚力と抗力
翼に作用する揚力Lおよび抗力Dは、次式で計算することができる。
$$L=\frac{1}{2}\rho U^2S・C_L$$
$$D=\frac{1}{2}\rho U^2S・C_D$$
ここで、\(\rho\)は流体の密度、\(C_L\)および\(C_D\)は揚力係数、抗力係数である。
また、揚力と抗力の比
$$\frac{L}{D}=\frac{C_L}{C_D}$$
を、揚抗比と呼び、翼の性能を表す指標として用いられる。
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]






