物体に働く力
理想流体中にある物体に働く力を求めるには、その物体まわりの圧力を積分すればよい。圧力は、ベルヌーイの式から得ることができる。
しかし、物体に働く力をいちいち圧力の積分により求めていては計算が煩雑である。そこで、物体に働く力を簡便に求める方法であるブラジウス(Blasius)の公式を導出する。
導出にあたり、複素関数の積分の知識が必要になるので、必要に応じてこちらを参照のこと。
ブラジウスの第一公式
まず、物体に働く「力」を求める。
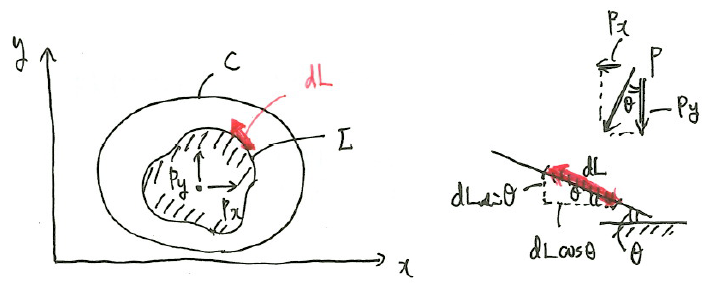
物体に働く\(x、y\)軸方向の力をそれぞれ\(P_x、P_y\)とする。物体の表面を表す滑らかな閉曲面を\(L\)とし、微小要素\(dL\)に働く力について考える。
上図より、
\[
\begin{cases}
dP_x=-pdL\sin\theta=-pdy \\
dP_y=-pdL\cos\theta=+pdx
\end{cases}
\]
これを物体周りで積分することで合力を得る。
$$P_x=-\oint_Lpdy ,P_y=\oint_Lpdx$$
ここで、2次元定常流のベルヌーイの式より
$$\frac{1}{2}U^2+gy+\frac{p}{\rho}=const$$
$$p=p_0-\frac{\rho}{2}(u^2+v^2)$$
と表せる。よって
さて、\(L\)の内部に特異点が存在しないとすると、定数\(p_0\)は正則関数なのでコーシーの積分定理により
$$-\oint_Lp_0dy=0 ,\oint_Lp_0dx=0$$
したがって、
となる。
物体表面は流線とみることができるので、\(dL\)について
$$udy=vdx$$
が成り立つ。これを用いると
\[
\begin{cases}
P_x=\displaystyle\frac{\rho}{2}\oint_L(2u^2-(u^2-v^2))dy=\frac{\rho}{2}\oint_L(2uvdx-(u^2-v^2)dy) \\
P_y=\displaystyle-\frac{\rho}{2}\oint_L((u^2-v^2)+2v^2)dx=-\frac{\rho}{2}\oint_L((u^2-v^2)dx+2uvdy)
\end{cases}
\]
したがって
\[
\begin{align*}
P_x-iP_y&=\frac{\rho}{2}\oint_L\{2uv(dx+idy)+(u^2-y^2)(idx-dy)\} \\
& =\frac{\rho}{2}\oint_L(u^2-v^2-i2uv)idz \\
& =i\frac{\rho}{2}\oint_L(u-iv)^2dz \\
& =i\frac{\rho}{2}\oint_L\left(\frac{dF(z)}{dz}\right)^2dz
\end{align*}
\]
最後に、コーシーの積分定理により、物体の外側を囲む(特異点を含まない)任意の閉曲線\(C\)での周回積分に書き換えて
$$P_x-iP_y=i\frac{\rho}{2}\oint_C\left(\frac{dF(z)}{dz}\right)^2dz$$
を得る。
これが、ブラジウスの第一公式である。
ブラジウスの第二公式
次に、物体に働く「モーメント」を求める。
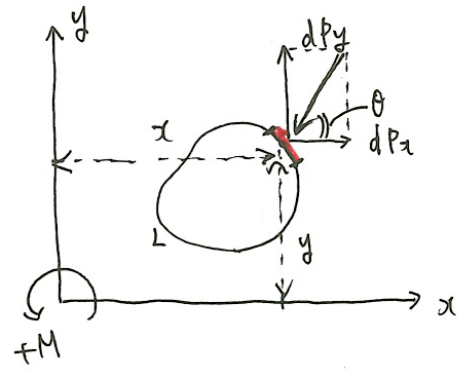
ブラジウスの第一公式のときと同様に
\[
\begin{cases}
dP_x=-pdy \\
dP_y=pdx
\end{cases}
\]
これらの力により発生する、原点回りのモーメント\(dM\)は次のようになる。
$$dM=xdP_y-ydP_x=p(xdx+ydy)$$
\[
\begin{align*}
M&=\oint_Lp(xdx+ydy) \\
& =\oint_Lp_0(xdx+ydy)-\frac{\rho}{2}\oint_L((u^2+v^2)xdx+(u^2+v^2)ydy) \\
& =-\frac{\rho}{2}\oint_L\{(u^2-v^2+2v^2)xdx-(2u^2-(u^2-v^2))ydy\} \\
& =-\frac{\rho}{2}\oint_L\{(u^2-v^2)(xdx-ydy)+2uv(xdx+ydy)\}
\end{align*}
\]
一方、共役複素速度の式より
\[
\begin{align*}
\left(\frac{dF(z)}{dz}\right)^2zdz&=(u-iv)^2(x+iy)(dx+idy) \\
& =(u^2-v^2)(xdx-ydy)+2uv(xdx+ydy) \\
& +i\{(u^2-v^2)(xdx+ydy)-2uv(xdx-ydy)\}
\end{align*}
\]
であるが、この実部と先の\(M\)の積分の中身が等しくなっている。よって
$$M=-\frac{\rho}{2}\oint_LRe\left[\left(\frac{dF(z)}{dz}\right)^2zdz\right]$$
から、コーシーの積分定理を適用して最終的に
$$M=-\frac{\rho}{2}Re\left[\oint_C\left(\frac{dF(z)}{dz}\right)^2zdz\right]$$
を得る。これを、ブラジウスの第二公式という。
ブラジウスの公式の変形
さて、ブラジウスの公式によって物体に働く力を求めることができるわけだが、積分を含む煩雑な計算を行う必要がある。
より実用的には、以下のような式変形をしておくとよい。
一般に、共役複素速度は
の形で記述できることが多い。よって
となるので、留数定理を適用すると
ブラジウスの第一公式:
\[
\begin{align*}
P_x-iP_y&=i\frac{\rho}{2}\oint_C\left(\frac{dF(z)}{dz}\right)^2dz \\
& =i\frac{\rho}{2}・2\pi i\mathrm{Res}_{z=0}\left(\frac{dF(z)}{dz}\right)^2 \\
& =-2\pi\rho A_0A_1
\end{align*}
\]
ブラジウスの第二公式:
より
\[
\begin{align*}
M&=-\frac{\rho}{2}Re\left[2\pi i(A_1^2+2A_0A_2)\right] \\
& =\pi\rho Im[A_1^2+2A_0A_2]
\end{align*}
\]
まとめ
$$\frac{dF(z)}{dz}=A_0+\frac{A_1}{z}+\frac{A_2}{z^2}+… のとき$$
$$(ブラジウスの第一公式): P_x-iP_y=-2\pi\rho A_0A_1$$
$$(ブラジウスの第二公式): M=\pi\rho Im[A_1^2+2A_0A_2]$$
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]






