ダランベールのパラドックスとは
完全流体が一様に流れている中に物体を置いたときに、物体には力が働かないということを「ダランベールのパラドックス(背理)」という。
もちろん実際には物体は流体から抵抗力が働く。しかし複素速度ポテンシャルを用いて計算すると、このような結論が得られてしまう。
今回は、このパラドックスを計算式から示していく。
流れ場の解析
平行流と2重吹き出しの組み合わせを考える。
複素速度ポテンシャルは、重ね合わせの原理により
\[
\begin{align*}
F(z)&=Uz+\frac{m}{2\pi z} \\
&=U(x+iy)+\frac{m}{2\pi}\left(\frac{x}{x^2+y^2}-i\frac{y}{x^2+y^2}\right)
\end{align*}
\]
\[
\begin{cases}
\phi=Ux+\frac{m}{2\pi}\frac{x}{x^2+y^2} \\
\psi=Uy-\frac{m}{2\pi}\frac{y}{x^2+y^2}
\end{cases}
\]
ψ=0となる流線は、
$$y=0$$
$$x^2+y^2=\frac{m}{2\pi U}=a_0^2 …(*)$$
となり、図示すると次のようになる。
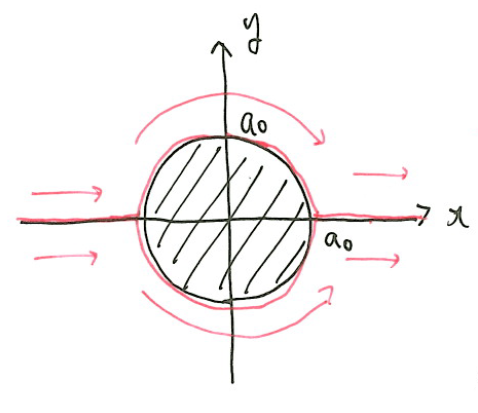
流線は固体壁と同等にみなすことができる。すなわち、原点に半径\(a_0\)の円柱を置いた状態に等しい。
$$z^2=r^2e^{2i\theta}=r^2(\cos 2\theta+\sin 2\theta)$$
を用いると、
\[
\begin{align*}
\frac{dF(x)}{dz}&=U-\frac{m}{2\pi z^2}=U-\frac{m}{2\pi r^2}e^{-2i\theta} \\
&=U-\frac{m}{2\pi r^2}\cos 2\theta+i\frac{m}{2\pi r^2}\sin 2\theta=u-iv
\end{align*}
\]
(※)式を用いて
となる。したがって、円柱壁面での速度は\(r=a_0\)として得られる。
\[
\begin{cases}
u=U(1-\cos 2\theta) \\
v=-U\sin 2\theta
\end{cases}
\]
円周方向の速度\(C_{\theta}\)は、
$$C_{\theta}=\sqrt{(u_{r=a_0})^2+(v_{r=a_0})^2}=|2U\sin\theta|$$
となる。これは、壁面における速度分布を表す。
さて、円柱に働く力を考えるために、圧力分布を求めよう。
無限遠での圧力を\(p_{\infty}\)、速度を\(U_{\infty}\)とする。無限遠では吹き出しの影響がなくなり、平行流のみとなるため、\(U_{\infty}=U\)である。
壁面での圧力を\(p\)とし、速度は\(C_{\theta}\)である。
これらからベルヌーイの式を立てると
$$\frac{1}{2}U_{\infty}^2+\frac{p_{\infty}}{\rho}=\frac{1}{2}C_{\theta}^2+\frac{p}{\rho}$$
上で求めた式を代入して整理すると、次式を得る。
上式がy軸について対称であることから、円柱壁は流体からの抵抗力を受けないことがわかる。
ただし実際には、流体の持つ粘性によって力を受けることになる。
これが、ダランベールのパラドックスである。
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]





