複素速度ポテンシャルとは
を用いて作られる次の関数\(F(z)\)を、複素速度ポテンシャルという。
$$F(z)=\phi(x,y)+i\psi(x,y)$$
複素関数の微分について、
\[
\begin{align*}
\frac{dF(z)}{dz} &=\lim_{\Delta x\to0}\left(\frac{\phi(x+\Delta x)-\phi(x)}{\Delta x}+i\frac{\psi(x+\Delta x)-\psi(x)}{\Delta x}\right) \\
&=\lim_{\Delta y\to0}\left(\frac{\phi(y+\Delta y)-\phi(y)}{i\Delta y}+i\frac{\psi(y+\Delta y)-\psi(y)}{i\Delta y}\right)
\end{align*}
\]
が成立することから、
$$\frac{dF(z)}{dz}=\frac{\partial\phi}{\partial x}+i\frac{\partial\psi}{\partial x}=-i\frac{\partial\phi}{\partial y}+\frac{\partial\psi}{\partial y}$$
これは、コーシー・リーマンの関係式そのものである。
結局、\(F(z)\)の微分は
$$\frac{dF(z)}{dz}=u-iv$$
となる。これを、共役複素速度という。
極座標系の場合、
\[
\begin{align*}
C_r-iC_{\theta}&=(u\cos\theta+v\sin\theta)-i(-u\sin\theta+v\cos\theta) \\
&=u(\cos\theta+i\sin\theta)-iv(\cos\theta+i\sin\theta) \\
&=e^{i\theta}(u-iv)
\end{align*}
\]
$$u-iv=e^{-i\theta}(C_r-iC_{\theta})$$
各種流れ場の複素速度ポテンシャル
いくつかの代表的な流れ場について、複素速度ポテンシャルを計算してみよう。
(1)一様な平行流
\[
\begin{cases}
u=U \\
v=0
\end{cases}
\]
すなわち
\[
\begin{cases}
\frac{\partial\phi}{\partial x}=\frac{\partial\psi}{\partial y}=U \\
\frac{\partial\phi}{\partial y}=-\frac{\partial\psi}{\partial x}=0
\end{cases}
\]
よって、
$$\phi=Ux , \psi=Uy$$
したがって、複素速度ポテンシャルは
(別解)
$$\frac{dF(z)}{dz}=u-iv=U$$
$$F(z)=Uz$$
(2)吹き出し
ある点からqの吹き出しがある場合を考える。
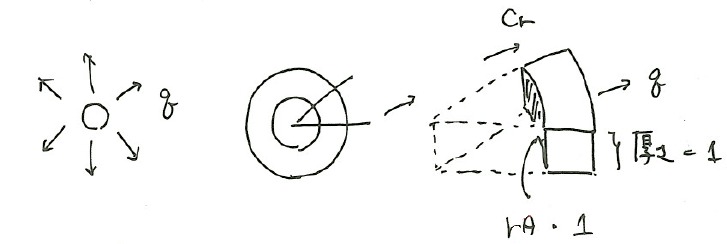
吹き出し量qは半径方向への流量を考えることで、
$$(2\pi r)・C_r=q$$
$$C_r=\frac{q}{2\pi r}$$
よって、
\[
\begin{cases}
C_r=\frac{q}{2\pi r} \\
C_{\theta}=0
\end{cases}
\]
\[
\begin{cases}
\phi=\frac{q}{2\pi}\ln{r} \\
\psi=\frac{q}{2\pi}\theta
\end{cases}
\]
したがって、
(別解)
$$F(z)=\frac{q}{2\pi}\ln{z}$$
(3)流体の円運動
円運動については、循環Γを用いる。
\(\mathbf{U}=(C_r, C_{\theta})、d\mathbf{l}=(dr, rd\theta)、C_r=0\)より、
$$\Gamma=\oint\mathbf{U}・d\mathbf{l}=\int_{0}^{2\pi}C_{\theta}・rd\theta=2\pi rC_{\theta}$$
\[
\begin{cases}
C_r=0 \\
C_{\theta}=\frac{\Gamma}{2\pi r}
\end{cases}
\]
\[
\begin{cases}
C_r=\frac{1}{r}\frac{\partial\psi}{\partial \theta}=\frac{\partial\phi}{\partial r} \\
C_{\theta}=-\frac{\partial\psi}{\partial r}=\frac{1}{r}\frac{\partial\phi}{\partial \theta}
\end{cases}
\]
よって、
$$\phi=\frac{\Gamma\theta}{2\pi} , \psi=-\frac{\Gamma}{2\pi}\ln{r}$$
となるので
(別解)
$$F(z)=-\frac{\Gamma i}{2\pi}\ln{z}$$
(4)吹き出しと吸い込み
\(z=-a\)に吹き出し(+q)、\(z=a\)に吸い込み(-q)があるとする。
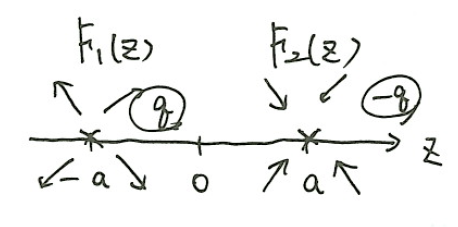
それぞれの複素速度ポテンシャルは、(2)吹き出しの項で求めた式から
\[
\begin{cases}
F_1(z)=\frac{q}{2\pi}\ln{(z+a)} \\
F_2(z)=-\frac{q}{2\pi}\ln{(z-a)}
\end{cases}
\]
重ね合わせの原理より、
$$F(z)=F_1(z)+F_2(z)$$
が成り立つ。したがって、
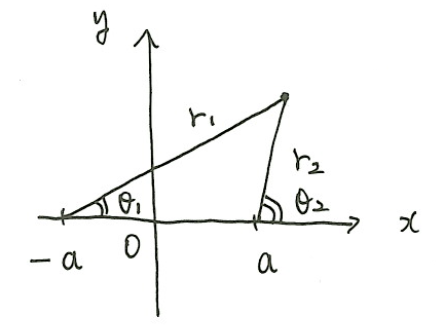
ここで、上図のように極座標を取ると
$$z+a=r_1e^{i\theta_1} , z-a=r_2e^{i\theta_2}$$
\[
\begin{align*}
F(z)&=\frac{q}{2\pi}\ln\frac{r_1e^{i\theta_1}}{r_2e^{i\theta_2}} \\
&=\frac{q}{2\pi}\ln\frac{r_1}{r_2}+i\frac{q}{2\pi}\ln(\theta_1-\theta_2)=\phi+i\psi
\end{align*}
\]
等ポテンシャル線は、\(\phi=\phi_0\)のときで、\(r_1/r_2=一定\)より
$$\left(\frac{r_1}{r_2}\right)^2=\frac{(x+a)^2+y^2}{(x-a)^2+y^2}=k(=const)$$
整理すると、
等ポテンシャル線は、x軸上に中心を持つ円群である。
一方、流線は\(\psi=\psi_0\)のときで、\(\theta_1-\theta_2=一定\)より
x=±aを通り、y軸上に中心を持つ円群である。
(5)2重吹き出し
(4)の\(F(z)\)について、マクローリン展開する。
$$F(z)=\frac{q}{2\pi}\ln{\frac{z+a}{z-a}}=\frac{q}{2\pi}\ln{\frac{1+\frac{a}{z}}{1-\frac{a}{z}}}$$
より
\[
\begin{align*}
F(z)&=\frac{q}{2\pi}\left[\frac{a}{z}+\frac{a}{z}-\frac{1}{2}\left(\frac{a}{z}\right)^2+\frac{1}{2}\left(\frac{a}{z}\right)^2+\frac{1}{3}\left(\frac{a}{z}\right)^3-\frac{1}{3}\left(\frac{a}{z}\right)^3-…\right] \\
&=\frac{q}{2\pi}\frac{2a}{z}
\end{align*}
\]
この式が成立するのは、aが非常に小さいとき、すなわち吹き出し点と吸い込み点がほぼ一致するときである。
このとき、
$$\phi=\frac{m}{2\pi}\frac{x}{x^2+y^2} , \psi-\frac{m}{2\pi}\frac{y}{x^2+y^2}$$
となる。
等ポテンシャル線はx軸上に中心を持つ円群、流線はy軸上に中心を持つ円群となり、流れは原点から出て原点に戻るイメージである。
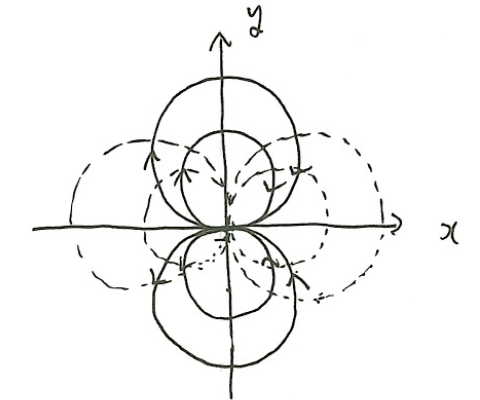
このとき、原点を2重吹き出し点、mを2重吹き出しの強さという。
(6)平行流と吹き出し
重ね合わせの原理
より、
$$F(z)=Uz+\frac{q}{2\pi}\ln{z}$$
\[
\begin{cases}
u=U+\frac{q}{2\pi}\frac{x}{x^2+y^2} \\
v=\frac{q}{2\pi}\frac{y}{x^2+y^2}
\end{cases}
\]
ここで、u=v=0となる点のことを、よどみ点と呼ぶ。
今回の場合、
$$U+\frac{q}{2\pi}\frac{x}{x^2+y^2}=\frac{q}{2\pi}\frac{y}{x^2+y^2}=0$$
から、よどみ点は
$$\left(-\frac{q}{2\pi U},0\right)$$
流体力学 連続方程式(質量保存則)の導出 オイラーの運動方程式(直交座標・極座標)の導出 流線の方程式と速度ポテンシャル・流れ関数の定義と関係式 ベルヌーイの定理(エネルギー保存則)の導出 流体の変形と回転・渦度と[…]





