はりに外力が作用すると、はりは変形してたわみが発生する。
ここでは、はりのたわみを表す曲線の方程式を導く。
たわみ\(y\)と、曲げモーメント\(M\)、ヤング率\(E\)、断面二次モーメント\(I_z\)の間に成り立つ関係式である。
はりの曲がり
曲線\(OPQN\)を、真直はり(荷重を受けないときに軸線が直線であるはり)に荷重が作用した後の軸線であるとする。
この曲線を、弾性曲線(elastic curve)あるいはたわみ曲線(deflection curve)という。
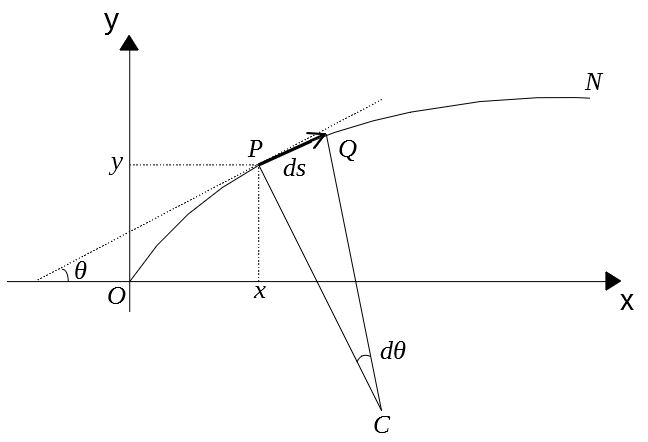
たわみ曲線上の点\(O\)を原点とした直交座標を取る。はりがたわむ前の軸線は\(x\)軸に一致しているとする。
たわみ曲線上に一点\(P\)をとり、その座標を\((x, y)\)とすると、\(P\)点におけるたわみは\(y\)となる。また、\(P\)における接線と\(x\)軸とがなす角を\(\theta\)とする。これをたわみ角という。
\(P\)の近くに点\(Q\)をとり、微小長さ\(ds=PQ\)をとる。\(P,Q\)における曲率半径のなす角を\(d\theta\)とする。交点\(C\)は曲率中心である。
点\(P\)における曲率半径を\(r\)とすると
$$ds=-rd\theta$$
$$\frac{1}{r}=-\frac{d\theta}{ds}$$
である。ここで、負号は次の意味を持つ。
たわみ曲線が下に凸になるように曲げモーメントが作用する場合を正とするため、曲率の中心がたわみ曲線よりも下にある場合、曲率\(1/r\)は負となる。
また、たわみ角は点\(P\)が正の方向(右)に移動するにつれて小さくなるので、\(ds\)の正に対して\(d\theta\)は負にとる。
たわみの方程式
曲率の式を\(x,y\)の式に書き換えていく。
$$\frac{1}{r}=-\frac{d\theta}{ds}=-\frac{d\theta}{dx}\frac{dx}{ds}$$
ここで、\(\tan\theta=dy/dx\)なので
$$\theta=\tan^{-1}\frac{dy}{dx}$$
$$\frac{d\theta}{dx}=\frac{\displaystyle\frac{d^2y}{dx^2}}{1+\displaystyle\left(\frac{dy}{dx}\right)^2}$$
また
したがって
\begin{align*}
\frac{1}{r}&=-\frac{\displaystyle\frac{d^2y}{dx^2}}{1+\displaystyle\left(\frac{dy}{dx}\right)^2}・\frac{1}{\sqrt{1+\displaystyle\left(\frac{dy}{dx}\right)^2}} \\
&=-\frac{\displaystyle\frac{d^2y}{dx^2}}{\left\{1+\displaystyle\left(\frac{dy}{dx}\right)^2\right\}^{\frac{3}{2}}}
\end{align*}
たわみ角\(\theta\)が小さいとき、分母≃1とできるので
$$\frac{1}{r}=-\frac{d^2y}{dx^2}$$
となる。
はりのせん断力を無視して、曲げモーメントのみが作用するとすれば、はりの曲げの式
$$\frac{1}{r}=\frac{M}{EI_z}$$
が成り立つ。したがって、次式を得る。
これを、はりのたわみの方程式という。
たわみの関係式
たわみの方程式をもとに、種々の関係式を導出することができる。
まず、たわみの方程式を\(x\)について積分すると、たわみ角を求めることができる。
$$\frac{dy}{dx}=\theta=-\int\frac{M}{EI_z}dx+C_1$$
もう一度\(x\)について積分すると、たわみを求めることができる。
$$y=\int\theta dx=-\iint\frac{M}{EI_z}dx^2+C_1x+C_2$$
あるいは、たわみの方程式を書き換えて
$$EI_z\frac{d^2y}{dx^2}=-M$$
これを\(x\)について微分すると、曲げモーメント\(M\)とせん断力\(F\)、分布荷重\(w\)の間には
$$\frac{dM}{dx}=F,\frac{dF}{dx}=\frac{d^2M}{dx^2}=-w$$
の関係があるので
$$EI_z\frac{d^3y}{dx^3}=-\frac{dM}{dx}=-F$$
$$EI_z\frac{d^4y}{dx^4}=-\frac{d^2M}{dx^2}=w$$
を得る。





