前回の記事では、集合の定義と元について書きました。今回は、集合の間の関係について解説していきます。
1.部分集合
集合が複数あるとき、それらの集合の間に成り立つ関係を次のように表現します。
$$ A \subset B$$
と表す
Aの元がすべてBの元である、というのは例えば次のような状態です。A={4の倍数}={4, 8, 12, …}、B={2の倍数}={2, 4, 6, …}としたとき、Aの元すなわち4の倍数はすべて2の倍数でもあることがわかるかと思います。このようなとき、集合Aは集合Bの一部分にあるイメージになります。
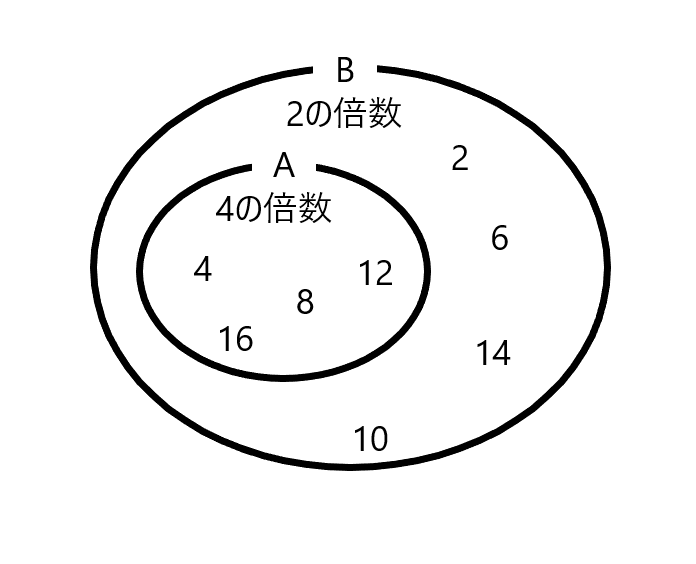
二つの集合について、互いが互いの部分集合であるとき、二つの集合は等しくなります。このことを次のように表します。
$$A \subset B かつ B \subset A$$
のとき
$$A=B$$
とかく
2.和集合と積集合
2.1 和集合
集合A, Bの少なくとも一方に含まれる元の全体からなる集合をA,Bの和集合(または合併)といい、
$$ A \cup B $$
とかく
和集合のイメージについては見たことがある方も多いかと思います。このように集合を図示する方法をベン図と呼びます。
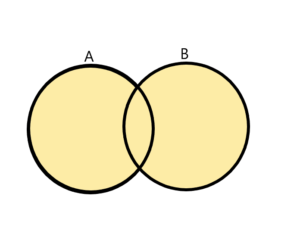
和集合の記号∪(カップ)の覚え方ですが、OR(または)の’O’を書くときに頭のところが少し開いているイメージで、と習った記憶があります。(伝わりにくい表現ですみません。。)
2.2 積集合
集合A, Bの両方に含まれる元の全体からなる集合をA,Bの積集合(または共通部分)といい、
$$A \cap B$$
とかく
積集合についても同様にベン図を書いてみると
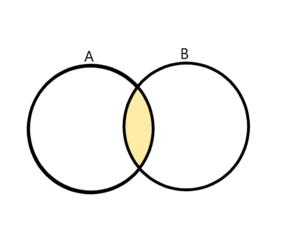
積集合の記号∩(キャップ)の覚え方ですが、AND(かつ)の’N’の小文字を書くときのイメージで、と習った記憶があります。
2.3 空集合
集合AとBが共通の元を持たない場合があります。すなわち、上の図でAとBが離れていて重なり部分がない場合、A∩Bは元を持ちません。このような集合を表現するために、「元を持たない集合」を空集合(くうしゅうごう)と定義し、Φ(ファイと読みます)で表します。
空集合Φは元を持たないので、あらゆる集合の部分集合であると約束することにします。
3.ド・モルガンの法則
3.1 補集合
集合について考えるとき、ひとつの大きな集合Uに対して部分集合Aを考えることが多くあります。確率でいうところの余事象のようなイメージでしょうか。
このような集合Uを、全体集合(または普遍集合)という。A⊂Uに対して、Aに属さないUの元の集合をAの補集合といい、
$$ \overline{A} または A^c$$
のようにあらわす
上つきのcは、complement(補集合)の頭文字です。
補集合の定義から、次が成り立ちます。ベン図を描いてみましょう。
$$ U=A \cup \overline{A}$$
3.2 ド・モルガン(De Morgan)の法則
それでは本題に入ります。ド・モルガンの法則は、集合や論理の否定などの基礎としてよく登場します。式だけでなく、ベン図を使うと理解しやすいと思います。
全体集合Uと、その部分集合A, Bがある。このとき、
$$ \overline{(A \cup B)}=\overline{A} \cap \overline{B}$$
$$ \overline{(A \cap B)}=\overline{A} \cup \overline{B}$$
が成り立つ
なんだか上線が出たり消えたりとよくわからないので、ベン図を描いてみましょう。
まず、A∪Bは2.1章のようにAかB少なくともいずれか一方でした。その補集合は、Uの中でA,Bに属さない部分全体を表しますので、次のように描くことができます。
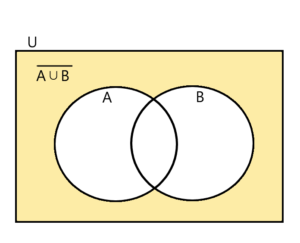
一方、Aの補集合は次のように描くことができます。
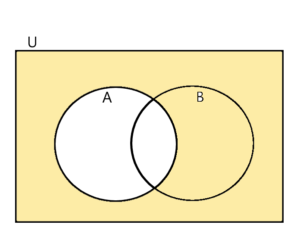
同じように、Bの補集合を描き、それぞれの共通部分(重なるところ)をとると、結局
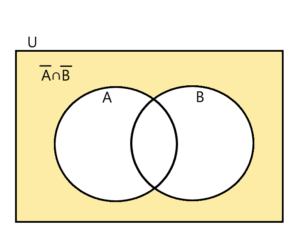
となり、最初のベン図と同じものができあがります。ド・モルガンの法則の第一式はこのことを表しているだけなのです。
第二式についてもベン図を描いて確認してみてください。





