自然数・整数・有理数・実数・複素数の定義と関係性

ふだん何気なく使っている数ですが、いろいろな分け方があります。

ここでは、集合(正確には環や体になりますが、簡単のため)の概念を借りて、数とその集合の大きさについて考えていきましょう。

自然数：ものを数えるときの数

例えばマラソンで順位を数えるとき、1着、2着、…と順に数えていきます。

このように、自然体でものを数えるときの数の集合\({1, 2, 3, \ldots}\)を「自然数(natural number)」と呼びます。

自然数には負の数は入りません。リンゴを数えるときに、「-2個ある！」ということは普通あり得ませんよね。(「0」を含めるかどうかについては分野や流儀にもよりますが、ここでは含めないものとします)

自然数の範囲内では、加法(足し算)と乗法(掛け算)を行うことができます。

2+3=5や3×5=15のように、自然数同士の足し算や掛け算を行って得られる結果もまた自然数になります。このことを’閉じている‘と表現することもあります。

整数：自然数に0と負の自然数を加えた数

負の自然数、という言葉を便宜上使いましたが、正確な表現ではありません。

0を基準にして1ずつ足したり引いたりしてできる数の集合\({0, 1, -1, 2, -2, 3, \ldots}\)として「整数(Integer)」は定義されます。この、\({-1, -2, -3,\ldots}\)のことを負の整数と表現することがあります。

整数の範囲内では、加法と乗法に加えて減法(引き算)を行うことができるようになります。

3-5=-2のように、自然数同士の引き算は自然数になるとは限りませんが、整数の範囲では計算することが可能になります。

このように、数の概念を拡張していくにつれて可能な演算の種類が増えていくわけです。まだ割り算を行うことができていないことにお気づきでしょうか。

有理数：ふたつの整数の比として表せる数

整数\(a, b\)を選んできて、\(a/b\)という分数を作ります(ただし、\(b≠0\)とします)。この\(a/b\)の形で表すことのできる数を「有理数(rational number)」と呼びます。

\(b=1\)とすれば、\(a/b=a\)となりますので、有理数は整数全体を含むことがわかります。

有理数の範囲まで拡大することで、ようやく加減乗除の四則演算すべてを行うことができるようになります。

実数：有理数と無理数を合わせた数

実数を定義する前に、無理数について定義しておきましょう。

無理数：二つの整数の比で表せない数

二つの整数の比として表せる数として有理数を定義しましたが、このように表すことのできない数ももちろんあります。例えば、\(\sqrt{2}\)などは分数の形で表すことができません(背理法で示すことができます)。そのような数のことを、「無理数(irrational number)」と呼びます。

無理数には、代数的無理数と超越数があります。詳細は別の機会にしますが、代数的数とは「有理数を係数にもつ一変数の多項方程式の解となりうるもの」であり、超越数はそれ以外のものです。超越数の代表例としては「円周率\(\pi\)」や「ネイピア数\(e\)」があります。

さて、有理数と無理数を合わせることで、数直線上の数すべてを表すことができるようになり、これを「実数(real number)」と呼びます。私たちが普段目にするものは基本的に実数の世界に存在する数です。

複素数：\(a+bi\)の形で表される数

最後に複素数です。

二つの実数\(a, b\)と、虚数単位\(i\)と呼ばれる元を持ってきて

$$z=a+bi$$

という数をつくる。ここで、$$i^2=-1$$とする。

\(b=0\)としたとき、\(z=a+0i=a\)は実数となります。したがって、複素数は実数を含みます。

これまでの数の定義を概念的に図示すると、次のようになります。

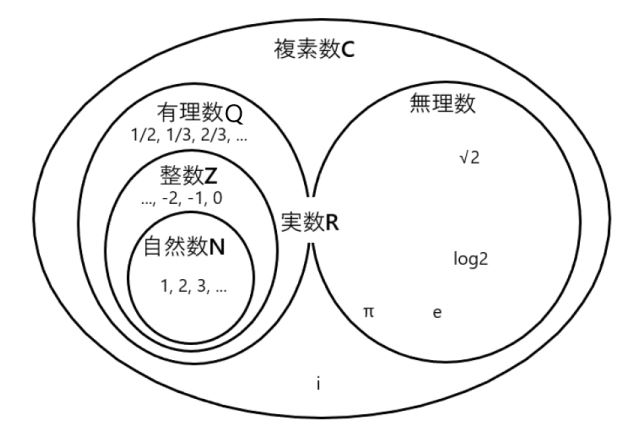
「複素数なんて、普段目にすることなんてないし存在しないんでしょ？」と思われる方もいるかもしれません。確かに、日常生活で複素数を意識して生活することはほとんどない(そんな人もいるのかもしれませんが)と思いますが、実は様々な分野で複素数は活躍しているのです。そのあたりの話もいずれ書いていけたらと思っています。

今回はここまで。

まとめページ

理工数学

線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー４つのパターン サラスの公式による行列式の計算方法 余因[…]