前回は、定積分の定義と積分可能性について学びました。(定積分①)
今回は、まずはじめに定積分に成り立つ性質および積分の平均値の定理について述べます。そして最後に、解析学の重要な定理である「微分積分学の基本定理」を示していきます。
微分積分学の基本定理により、微分と積分が逆演算であることが示されます。
定積分の性質
\(a≧b\)のとき
$$\int_a^a f(x)dx=0$$
$$\int_a^b f(x)dx=-\int_b^a f(x)dx$$
と規約します。
①区間と可積
\(fを[a,b]\)で可積とすると、\([a,b]\)に含まれる任意の閉区間で可積である。
②区間加法性
\(fが[a,b]および[b,c](a<b<c)\)で可積とすると、\([a,c]\)でも可積となり次式が成立する。
$$\int_a^c f(x)dx=\int_a^b f(x)dx+\int_b^c f(x)dx$$
③定積分の線形性
\(f,gをI=[a,b]\)で可積とすると、\(f\pm g、kf(k:定数)、fg\)も可積である。
また、\(\alpha, \beta\)を定数として次式が成り立つ。
④関数と定積分の大小関係
\(f(x)、g(x)が[a,b]\)上で可積かつ\(f(x)\le g(x)\)とすると
さらに\(f(x)、g(x)\)がともに連続ならば、等号は\(f(x)\equiv g(x)\)のときのみ成り立つ。
とくに、\(f(x)が[a,b]\)上で可積かつ\(f(x)\ge 0\)とすると
$$\int_a^b f(x)dx\ge 0$$
さらに\(f(x)\)が連続ならば、等号は\(f(x)\equiv 0\)のときのみ成り立つ。
⑤定積分と絶対値
$$\left|\int_a^b f(x)dx \right| \le \int_a^b |f(x)|dx$$
積分の平均値定理
微分で学んだ平均値の定理(ラグランジュの平均値の定理・コーシーの平均値の定理)と同様に、積分にも平均値の定理があります。
\(f(x)は[a,b]\)上で可積とし、\(m\le f(x)\le M\)とする。このとき、
を満たす\(\lambda\)が存在する。\(f(x)が[a,b]\)で連続ならば、
$$\lambda=f(c)となるc(a<c<b)$$
が存在する。
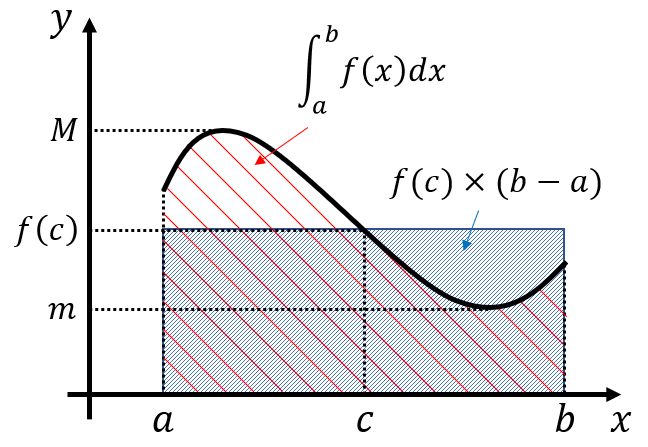
積分の平均値の定理(連続関数の場合)を図に示すと上のようになります。
(証明)
\(m\le f(x)\le M\)より
$$\int_a^b mdx\le \int_a^b f(x)dx\le \int_a^b Mdx$$
$$m(b-a)\le \int_a^b f(x)dx \le M(b-a)$$
$$m\le \frac{1}{b-a}\int_a^b f(x)dx \le M$$
となる。中間値の定理より、
$$f(c)=\frac{1}{b-a}\int_a^b f(x)dx (a<c<b)$$
となる数\(c\)が\(aとb\)の間に存在する。
(証明終)
不定積分と定積分
\(f(x)はI=[a,b]\)上で可積とする。定積分の性質①より、\(I\)上の関数
$$F(x)=\int_a^x f(t)dt (a\le x\le b)$$
が定義される。この関数をfの不定積分と呼ぶ。
定理:不定積分の連続性
\(f(x)がI=[a, b]\)上で可積とすると、その不定積分\(F(x)\)は\(I\)上で連続である。
(証明)
\(f\)は有界なので、\(|f(x)|\le M\)とする。定積分の性質②④⑤より
$$\left| \int_x^{x+h} Mdt \right|=M|h|$$
\(h\to0\)とすれば、\(F(x+h)-F(x)\to0\)を得る。
(証明終)
定理:不定積分の微分
\(f(x)がI=[a,b]\)上で可積、\(I\)の1点\(x=x_0\)で連続とする。このとき、\(f(x)\)の不定積分\(F(x)\)は\(x=x_0\)で微分可能で、
$$F'(x_0)=f(x_0)$$
が成り立つ。
(証明)
$$\frac{F(x_0+h)-F(x_0)}{h}=\frac{1}{h}\int_{x_0}^{x_0+h} f(t)dt$$
および積分に関する平均値定理より
\([x_0, x_0+h]\) (または\([x_0+h, x_0]\))における\(f\)の上限、下限をそれぞれ\(M(h)、m(h)\)とすると
とおける。仮定より、\(h\to0\)のとき\(m(h)、M(h)\to f(x_0)\)となるので、\(\lambda(h)\to f(x_0)\)
$$ゆえに、F'(x_0)=f(x_0)$$
(証明終)
\(fが[a, b]\)で連続ならば、そこで原始関数をもちます。
微分積分学の基本定理
\(f(x)がI=[a,b]\)上で可積、かつ\(I\)上で原始関数\(G(x)\)をもつならば
$$\int_a^b f(x)dx=[G(x)]_a^b\equiv G(b)-G(a)$$
(証明)
\(I\)のn等分割\(\Delta\)をとる。微分に関する平均値の定理により、各小区間で
よって、
\[
\begin{align*}
G(b)-G(a)&=\sum_{k=1}^n (G(x_k)-G(x_{k-1})) \\
&=\sum_{k=1}^n f(\xi_k)\Delta x_k
\end{align*}
\]
\(n\to\infty\)とするとき、最後の項は
$$\int_a^b f(x)dx$$
に収束する。
(証明終)
これで無事に微分と積分の関係を導くことができました。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]




