この記事から数回にわたって、定積分について学んでいきます。
不定積分についてはこちら ⇒ 不定積分の定義と公式、有理関数・三角関数・無理関数の不定積分
定積分
リーマン和
定積分の始まりは、「細かく分けて足し合わせる」ことです。計算も大切ですが、そもそもの考え方を理解しておきましょう。
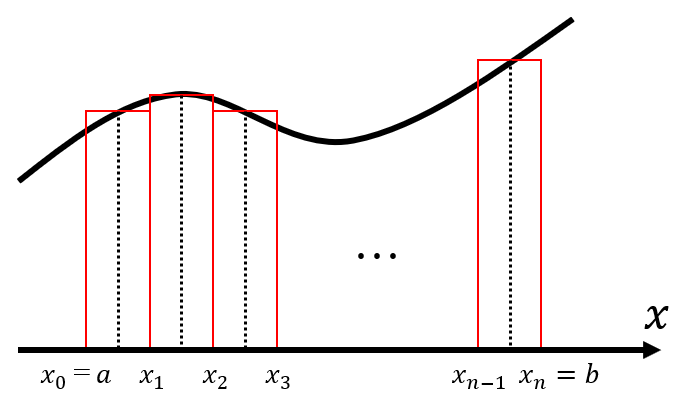
$$f(x)を閉区間I=[a, b]上の有界な関数とする。Iをいくつかの小区間に分け、その分点を$$
$$a=x_0<x_1<x_2<…<x_n=bとする。この分割\Deltaに対して$$
$$I_k=[x_{k-1}, x_k] \Delta x_k=x_k-x_{k-1} (k=1,2,…,n)$$
$$とおき、|\Delta|=\max_{1\le k\le n}\Delta x_kを分割\Deltaの幅という$$
さらに、各小区間Ikの中から任意の点ξkを選び、長方形を作って足し合わせます。
$$R[\Delta ; \{\xi _k\}]=\sum_{k=1}^{n} f(\xi _k)\Delta x_k$$
これを、Δ, {ξk}に関するfのリーマン和といいます。
リーマン積分可能
分割を限りなく細かくしていくとき、分割Δおよび{ξk}の取り方に関係なくリーマン和がある定数Jに近づくとき、すなわち
$$|\Delta|\to 0 ならば R[\Delta ; \{\xi _k\}]\to J$$
であるとき、fはI上でリーマン積分可能(または可積)であるといいます。
このとき値JをfのI上の定積分とよび、
$$\int_a^b f(x)dx$$
と表します。
積分可能性の判定条件
便利のため、次の量を導入します。
$$区間I_kでのfの上限、下限をそれぞれM_k、m_kとおき、分割\Deltaに対して$$
$$S[\Delta]=\sum_{k=1}^n M_k\Delta x_k$$
$$s[\Delta]=\sum_{k=1}^n m_k\Delta x_k$$
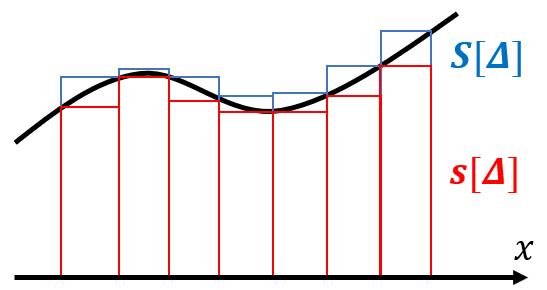
上図の赤い四角形の面積の和がs[Δ]で、それより大きい青い四角形の面積の和がS[Δ]を表します。図より明らかに、
$$s[\Delta]\le R[\Delta ; \{\xi _k\}]\le S[\Delta]$$
区間の細分と下積分・上積分
分割Δ、Δ’について、Δの分点がすべてΔ’の分点になっているとき、Δ’はΔの細分であるといいます。このとき、次が成立します。
$$s[\Delta]\le s[\Delta’]、S[\Delta]\ge S[\Delta’]$$
二つの分割Δ1、Δ2に対して、両方の分点を採用して得られる分割をΔ1∪Δ2とかきます。当然これはΔ1、Δ2の細分になっているので
$$s[\Delta_1]\le s[\Delta_1\cup \Delta_2]\le S[\Delta_1\cup \Delta_2]\le S[\Delta_2]$$
したがって、任意の分割Δ1、Δ2に対して
$$s[\Delta_1]\le S[\Delta_2]$$
となります。そこで
$$s=\sup_\Delta s[\Delta]、S=\inf_\Delta S[\Delta]$$
とおくと、s≦Sとなります。このs、SをそれぞれfのI上の下積分、上積分と呼びます。
ダルブーの定理
$$fをI上の有界関数とするとき、次が成立する$$
$$|\Delta|\to 0のとき、S[\Delta]\to S、s[\Delta]\to s$$
I上の有界関数fがI上で積分可能となるための条件は、s=Sが成り立つことです。
この条件を使いやすくするために、さらに次の量を導入します。
$$分割\Deltaの各区間I_kに対し$$
$$\omega(I_k; f)=\omega_k=\sup\{ f(x)-f(x’)|x,x’\in I_k \}$$
$$とおき、これをI_kにおけるfの振動量と呼ぶ。$$
$$\omega_k=M_k-m_k (M_k=\sup_{I_k}f、m_k=\inf_{I_k}f)$$
$$であるので、S[\Delta]-s[\Delta]=\sum_{k=1}^n \omega_k\Delta x_k$$
積分可能条件
$$I上の有界関数fがI上で積分可能となるための条件は、任意の正数\epsilonに対し$$
$$\sum_{k=1}^n \omega_k\Delta x_k <\epsilonを満たすIの分割Δが存在することである$$
$$[a,b]上の単調関数f(x)は積分可能です$$
$$I=[a,b]上の連続関数f(x)は積分可能です$$






