ロルの定理とラグランジュの平均値定理の証明

今回は、微分で登場する「平均値の定理」について学習していきます。

「微分の計算はよくわかったけど、平均値の定理って意味合いがよくわからないなあ」「これ何に使うの？」と思う人も少なくないと思います。そこでこの記事では、平均値の定理の意味合いとその証明をしていきます。

なお、ここでいう平均値の定理は「ラグランジュの平均値の定理」のことであり、その拡張である「コーシーの平均値の定理」については別記事で解説していますので、ご参照ください。

ラグランジュの平均値の定理の概要

まずは定理を述べておきます。

さて、この定理は一体何を主張しているのでしょうか？図にするとわかりやすいので、下図のような状況を考えてみることにします。

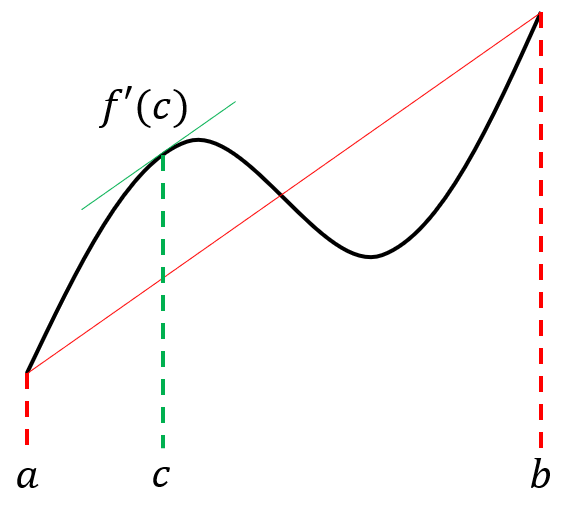
関数$f(x)$が図のような曲線を表すとします。どんな形でも構いませんが、区間$[a,b]$で連続かつ点$a,b$を除いて微分可能(滑らか)である必要があります。

定理の左辺は、2点$(a, f(a)), (a, f(b))$を結ぶ線分(赤の実線)の傾きに他なりません。一方、定理の右辺は、点$(c, f(c))$における接線(緑の実線)の傾きを表しています。この両者が等しくなるような$c$が存在する、というのがラグランジュの平均値の定理の意味するところです。

言い換えると、「曲線の両端を結んだ線の傾きと並行な接線を曲線上に引くことができる」ということです。引ける接線の本数は何本でも構いません。

ロルの定理と証明

さて、平均値の定理を証明したいと思います。が、その前に準備として次の「ロルの定理(Rolle’s theorem)」を示しておく必要があります。

平均値の定理より少し条件が厳しくなっています。$f(a)=f(b)$なので、上の図で赤線がx軸に平行になる場合を考えていることになります。

(証明)

(ⅰ)　$f(x)$が定数のとき、$f'(x)=0$なので任意の$c$について成立する。

(ⅱ)　$f(x)$が定数でないとき、まず$f(a)=f(b)$より大きい値をとる場合について考える。

$f(x)$は$[a,b]$において最大値をとるが、それが$x=c$のときであるとすると、$c\not =a,b$かつ$f'(c)=0$であることを示せばよい。

$a\le x \le b$で$f(x)-f(c)\le 0$であるから、$\frac{f(x)-f(c)}{x-c}$の値は、

$a<x<c$のとき、$\ge 0$，　$c<x<b$のとき、$\le 0$である。

よって、$x\to c-0，x\to c+0$とすることにより$f'(c)\ge 0$かつ$f'(c)\le 0$、すなわち$f'(c)=0$を得る。

$f(a)=f(b)$より小さい値をとる場合については、$-f$を考えればよい。

(証明終)

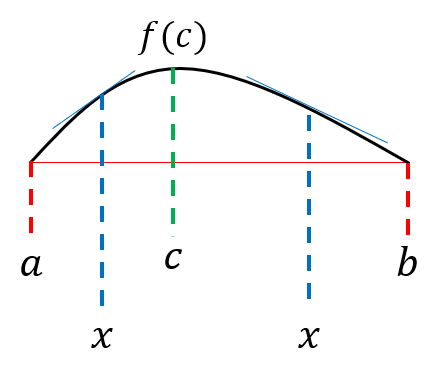
少しだけ補足説明をします。

(ⅱ)の状況を簡単に表すと図のようになります。このとき、最大値をとる点$(c,f(c))$における接線の傾きが0であることを示すことが目的です。

$x\to c$となるときの微分係数を求めればよいのですが、$x\to c$の近づけ方は小さい側からと大きい側からの2通りがあります。

最大値は$f(c)$なので$f(x)-f(c)$は常に0以下になりますから、$x-c$の符号を考えればよいです。

いずれにせよ限りなく0に近づいていきます。このことは、「ある範囲内で最大値をとる点における接線の傾きは0である」ということを示しています。

平均値の定理の証明

ようやく本題ですが、前項のロルの定理の証明が実は山場であり、平均値の定理の証明はすでにほとんど終わっています。

(証明)

次の関数に対し、ロルの定理を適用すればよい。

(証明終)

まとめ

今回は、ロルの定理と平均値の定理について紹介していきました。実はこれで終わりではなく、この後にテイラーの定理やロピタルの定理といった有名かつ重要な定理を示していくことができるようになりました。

この後の記事では、それらについて学習していきたいと思います。

まとめページ

理工数学

線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー４つのパターン サラスの公式による行列式の計算方法 余因[…]