前回の記事でシンプレックス法の基本手順について学んだ。
[mathjax] この記事では、線形計画法の代表的な解法であるシンプレックス法について解説する。 線形計画法では、ある制約条件の下で目的関数を最大化または最小化することを考える。 高校数学においても、[…]
シンプレックス法を適用するにあたり
- 等式の制約条件
- 不等号の向きが反対
- \(b_i\)が負
- 変数に符号の制約がない
のような場合、技巧変数\(\nu\)や係数\(M\)を用いて制約条件の書き換えを行った。
このような解法の例として罰金法の例題を紹介した。
これに対して、コンピュータを用いて線形計画問題を解く場合によく用いられる方法が2段階シンプレックス法である。
以下では、2段階シンプレックス法の基本と解法を学ぶ。
2段階のシンプレックス法
2段階のシンプレックス法では、スラック変数を用いて標準形に変換するだけで計算することが可能であるという利点がある。
次の2つのフェーズからなる。
Phase 1 一般の基底解を実行可能な基底解に変換する手順
第一段階は技巧変数等で対応していた部分であり、実行可能な基底解を得るために基底変換を行う。
Phase 2 実行可能な基底解から最適解に到達する手順
第二段階は通常のシンプレックス法の計算である。
さて、2段階のシンプレックス法の計算手順を見ていこう。
STEP1 シンプレックス判定を行う
基底変数\(b_i\)が負である行の集合を\(N\)とするとき、次のシンプレックス基準を計算する。
$$\omega_j=\sum_{i\in N}a_{ij}^{(h)}$$
非基底変数のうち\(\omega_j\lt0\)なるものが存在すれば次のSTEPへ進む。そうでなければ、実行可能な基底解は存在しないので終了する。
STEP2 基底に入れる変数を決める
最小の\(\omega_j\)を与える変数\(x_k\)を基底に入れる。
STEP3 基底から除く変数を決める
\(b_i^{(h)}\ge0,a_{ik}^{(h)}\gt0\)である\(i\)に対して最小の増加限界\(\theta_i=b_i^{(h)}/a_{ik}^{(h)}\)を与える変数\(x_l\)を基底から取り除く。
このような\(i\)が存在しない場合は、\(b_i^{(h)}\lt0,a_{ik}^{(h)}\lt0\)である\(i\)に対して最大の増加限界\(\theta_i=b_i^{(h)}/a_{ik}^{(h)}\)を与える変数\(x_l\)を基底から取り除く。
STEP4 基底変換を行う
\((l,k)\)要素をピボットとして掃き出し計算を行い、新しいシンプレックス表を作成する。
STEP5 実行可能性を判定する
新しい基底解について、すべての\(b_i^{(h+1)}\ge0\)であれば実行可能な基底が得られたためPhase1は終了する。
そうでなければSTEP1に戻って繰り返す。
実際に2段階シンプレックス法を用いて計算をしてみよう。
例題
次の線形計画問題を、シンプレックス法を用いて解け。
\mathrm{Minimize} & z=2x_1+19x_2+7x_3 \\
\mathrm{subject~to} & x_1+12x_2+6x_3\ge4 \\
& 2x_1+18x_2+4x_3\ge3 \\
& x_1,x_2,x_3\ge0
\end{align*}\]
不等号の向きが逆なので、従来の解法であればスラック変数\(\lambda\)と技巧変数\(\nu\)を導入して解き進める必要がある。
これに対し、2段階のシンプレックス法を適用する場合はスラック変数のみを導入すればよい。
(解)
サイクル0のタブローは次のようになる。

基底変数の値が負なので、実行可能な基底解ではない。よってPhase 1の計算を行う。
まずはシンプレックス基準を求める。
$$\omega_j=\sum_{i\in N}a_{ij}^{(h)}$$
この中で最小の\(\omega_j\)を与える\(x_2\)を新たに基底変数に入れる。

次に増加限界\(\theta_i=b_i^{(h)}/a_{i2}^{(h)}\)を計算する。
\(b_i\)がともに負であるので、最大の増加限界を与える変数\(\lambda_1\)を基底から取り除く。
\((1,2)\)要素をピボットにして掃き出し計算を行うと、以下のようになる。

ここで、基底変数の値がすべて性になったので、これは実行可能な基底解になっている。
よってPhase 1を終了し、ここから通常のシンプレックス計算であるPhase 2へ移行する。
最終的に以下のシンプレックス・タブローを得る。
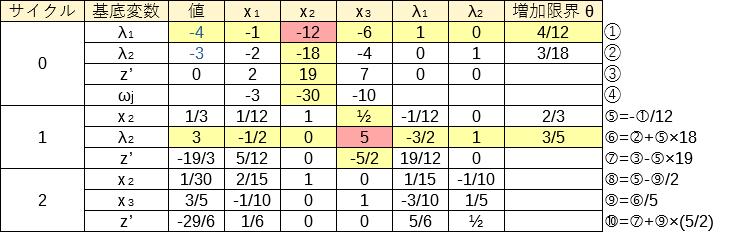
したがって、\(x_1=0,x_2=1/30,x_3=3/5\)のとき、最小値\(z=29/6\)となる。
以上が2段階のシンプレックス法による計算である。
罰金法を使う場合に比べ、導入する変数が少なくて済んでいることがわかるだろう。
線形代数学 内積の定義と正値性・対称性・線形性について 特別な行列の名前と定義・性質の一覧 対称行列と反対称行列の性質・分解公式 行列のn乗の計算方法ー4つのパターン サラスの公式による行列式の計算方法 余因[…]